toes.png

Distort it.
%IMG7%magick ^ toes.png ^ +level 5,92%% ^ gbl_samp1.png

Converting between parameters for -level, +level and gain-and-bias.
Linear transformations can be applied by gain and bias, or two parameters to "-level", or two parameters to "+level". These methods are equivalent. If we know the parameters for one method, we can calculate the parameters for the other two methods.
ASIDE. This page is one of a series that address the question: "What colour transformation makes this image look like that image?"
The pages in that series, roughly from simple to complex, are:
The diagram illustrates the situation. From the origin (0,0), the x-axis is input image values, and the y-axis is output image values. The central square is input and output values in the range 0 to 100%. The blue line is a transformation from input to output, which can be implemented by "-level L1,L2%" or "+level L3p,L4p%" or "-function Polynomial gain,bias".
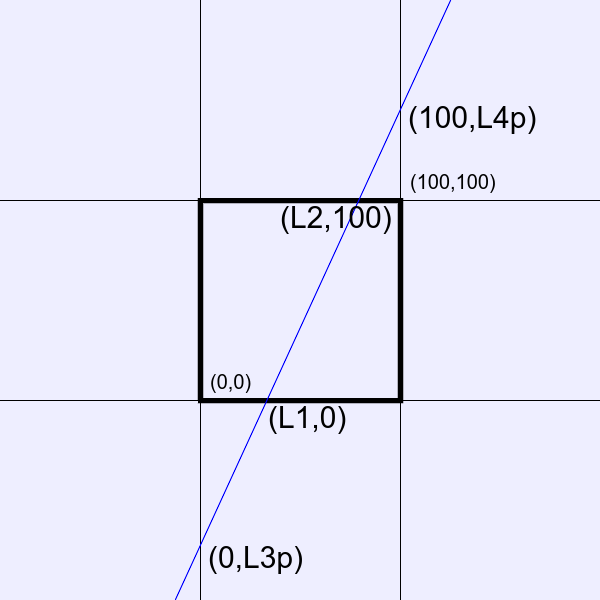
gain is the slope of the blue line, dy/dx, and bias = L3p/100.
Six scripts are provided, for conversion from any of the three methods to any of the others. The scripts are concerned only with the six parameters; they do no image processing.
|
toes.png |

|
|
Distort it. %IMG7%magick ^ toes.png ^ +level 5,92%% ^ gbl_samp1.png |

|
Find the gain and bias parameters. See What level?.
call %PICTBAT%linReg2img toes.png gbl_samp1.png gbl_params
From the gain and bias parameters, calculate the level parameters:
call %PICTBAT%gbToL1L2 gbl_params call %PICTBAT%gbToL3pL4p gbl_params
List the parameters:
set gbl_params
gbl_params_bias_B=0.0500003278305486 gbl_params_bias_G=0.0500002682249943 gbl_params_bias_R=0.0499994933527886 gbl_params_gain_B=0.869999451628901 gbl_params_gain_G=0.869999630445563 gbl_params_gain_R=0.870001120584421 gbl_params_L1_B=-5.7471677409604 gbl_params_L1_G=-5.74715970849172 gbl_params_L1_R=-5.74706079909432 gbl_params_L2_B=109.195433444328 gbl_params_L2_G=109.195417851899 gbl_params_L2_R=109.195319887525 gbl_params_L3p_B=5.00003278305486 gbl_params_L3p_G=5.00002682249943 gbl_params_L3p_R=4.99994933527886 gbl_params_L4p_B=91.999977945945 gbl_params_L4p_G=91.9999898670557 gbl_params_L4p_R=92.000061393721
Apply the parameters with the three methods:
|
With "-function Polynomial". %IM7DEV%magick ^ toes.png ^ -channel R ^ -function Polynomial %gbl_params_gain_R%,%gbl_params_bias_R% ^ -channel G ^ -function Polynomial %gbl_params_gain_G%,%gbl_params_bias_G% ^ -channel B ^ -function Polynomial %gbl_params_gain_B%,%gbl_params_bias_B% ^ +channel ^ gbl_distgb.png |

|
|
With "-function Polynomial", kludge fix. %IMG7%magick ^ toes.png ^ -channel R ^ -evaluate Multiply %gbl_params_gain_R% ^ -evaluate Add %%[fx:%gbl_params_bias_R%*QuantumRange] ^ -channel G ^ -evaluate Multiply %gbl_params_gain_G% ^ -evaluate Add %%[fx:%gbl_params_bias_G%*QuantumRange] ^ -channel B ^ -evaluate Multiply %gbl_params_gain_B% ^ -evaluate Add %%[fx:%gbl_params_bias_B%*QuantumRange] ^ +channel ^ gbl_distgb_k.png |

|
|
With "-level". %IMG7%magick ^ toes.png ^ -channel R ^ -level %gbl_params_L1_R%,%gbl_params_L2_R%%% ^ -channel G ^ -level %gbl_params_L1_G%,%gbl_params_L2_G%%% ^ -channel B ^ -level %gbl_params_L1_B%,%gbl_params_L2_B%%% ^ +channel ^ gbl_levm.png |

|
|
With "+level". %IMG7%magick ^ toes.png ^ -channel R ^ +level %gbl_params_L3p_R%,%gbl_params_L4p_R%%% ^ -channel G ^ +level %gbl_params_L3p_G%,%gbl_params_L4p_G%%% ^ -channel B ^ +level %gbl_params_L3p_B%,%gbl_params_L4p_B%%% ^ +channel ^ gbl_levp.png |

|
How different are these results?
%IMG7%magick compare -metric RMSE gbl_distgb.png gbl_distgb_k.png NULL:
0.0508194 (7.75454e-07)
%IMG7%magick compare -metric RMSE gbl_distgb_k.png gbl_levm.png NULL:
0.0511871 (7.81065e-07)
%IMG7%magick compare -metric RMSE gbl_distgb_k.png gbl_levp.png NULL:
0.0511871 (7.81065e-07)
%IMG7%magick compare -metric RMSE gbl_levm.png gbl_levp.png NULL:
0 (0)
The "-level" and "+level" methods are identical, and virtually identical to the gain-and-bias kludge method.
%IMG7%magick compare -metric RMSE gbl_samp1.png gbl_distgb_k.png NULL:
0.0801188 (1.22253e-06)
%IMG7%magick compare -metric RMSE gbl_samp1.png gbl_levm.png NULL:
0.078258 (1.19414e-06)
Instead of "level", we could use "level-colors".
For convenience, .bat scripts are also available in a single zip file. See Zipped BAT files.
rem Converts from gain and bias (nominal 0 to 1) to "-level L1,L2%" (nominal 0 to 100) rem %1 is prefix for environment variable. rem gain = -bias/(L1/100) rem L2-L1 = 100/gain rem L2 = L1 + 100/gain set FMT=^ %1_L1_R=%%[fx:-(!%1_bias_R!/!%1_gain_R!*100)]\n^ %1_L2_R=%%[fx:-(!%1_bias_R!/!%1_gain_R!*100)+100/!%1_gain_R%!]\n^ %1_L1_G=%%[fx:-(!%1_bias_G!/!%1_gain_G!*100)]\n^ %1_L2_G=%%[fx:-(!%1_bias_G!/!%1_gain_G!*100)+100/!%1_gain_G%!]\n^ %1_L1_B=%%[fx:-(!%1_bias_B!/!%1_gain_B!*100)]\n^ %1_L2_B=%%[fx:-(!%1_bias_B!/!%1_gain_B!*100)+100/!%1_gain_B%!]\n for /F "usebackq" %%L in (`%IMG7%magick identify ^ -precision 15 ^ -format "%FMT%" ^ xc:`) do set %%L
rem Converts from gain and bias (nominal 0 to 1) to "+level L3p,L4p%" (nominal 0 to 100) rem %1 is prefix for environment variable. rem L3p=bias*100 rem gain=(L4p-L3p)/100 rem gain*100=L4p-L3p=L4p-bias*100 rem L4p=(bias+gain)*100 set FMT=^ %1_L3p_R=%%[fx:!%1_bias_R!*100]\n^ %1_L3p_G=%%[fx:!%1_bias_G!*100]\n^ %1_L3p_B=%%[fx:!%1_bias_B!*100]\n^ %1_L4p_R=%%[fx:(!%1_bias_R!+!%1_gain_R!)*100]\n^ %1_L4p_G=%%[fx:(!%1_bias_G!+!%1_gain_G!)*100]\n^ %1_L4p_B=%%[fx:(!%1_bias_B!+!%1_gain_B!)*100]\n for /F "usebackq" %%L in (`%IMG7%magick identify ^ -precision 15 ^ -format "%FMT%" ^ xc:`) do set %%L
rem Converts from "-level L1,L2%" (nominal 0 to 100) to gain and bias (nominal 0 to 1) rem %1 is prefix for environment variable. rem gain=100/(L2-L1) rem bias=-gain*L1 set FMT=^ %1_gain_Rx=%%[fx:100/(!%1_L2_R!-!%1_L1_R!)]\n^ %1_gain_Gx=%%[fx:100/(!%1_L2_G!-!%1_L1_G!)]\n^ %1_gain_Bx=%%[fx:100/(!%1_L2_B!-!%1_L1_B!)]\n^ %1_bias_Rx=%%[fx:-(!%1_L1_R!)/(!%1_L2_R!-!%1_L1_R!)]\n^ %1_bias_Gx=%%[fx:-(!%1_L1_G!)/(!%1_L2_G!-!%1_L1_G!)]\n^ %1_bias_Bx=%%[fx:-(!%1_L1_B!)/(!%1_L2_B!-!%1_L1_B!)]\n for /F "usebackq" %%L in (`%IMG7%magick identify ^ -precision 15 ^ -format "%FMT%" ^ xc:`) do set %%L
rem Converts from "+level L3p,L4p%" (nominal 0 to 100) to gain and bias (nominal 0 to 1) rem %1 is prefix for environment variable. rem bias=L3p/100 rem gain=(L4p-L3p)/100 set FMT=^ %1_bias_Ry=%%[fx:!%1_L3p_R!/100]\n^ %1_bias_Gy=%%[fx:!%1_L3p_G!/100]\n^ %1_bias_By=%%[fx:!%1_L3p_B!/100]\n^ %1_gain_Ry=%%[fx:(!%1_L4p_R!-!%1_L3p_R!)/100]\n^ %1_gain_Gy=%%[fx:(!%1_L4p_G!-!%1_L3p_G!)/100]\n^ %1_gain_By=%%[fx:(!%1_L4p_B!-!%1_L3p_B!)/100]\n for /F "usebackq" %%L in (`%IMG7%magick identify ^ -precision 15 ^ -format "%FMT%" ^ xc:`) do set %%L
rem Converts from "-level L1,L2%" to "+level L3p,L4p%" (nominal 0 to 100) rem %1 is prefix for environment variable. call %PICTBAT%L1L2toGb %1 if ERRORLEVEL 1 exit /B 1 call %PICTBAT%gbToL3pL4p %1 if ERRORLEVEL 1 exit /B 1
rem Converts from "-level L3p,L4p%" to "+level L1,L2%" (nominal 0 to 100) rem %1 is prefix for environment variable. call %PICTBAT%L3pL4ptoGb %1 if ERRORLEVEL 1 exit /B 1 call %PICTBAT%gbToL1L2 %1 if ERRORLEVEL 1 exit /B 1
All images on this page were created by the commands shown, using:
%IMG7%magick identify -version
Version: ImageMagick 7.1.1-15 Q16-HDRI x64 a0a5f3d:20230730 https://imagemagick.org Copyright: (C) 1999 ImageMagick Studio LLC License: https://imagemagick.org/script/license.php Features: Cipher DPC HDRI OpenCL OpenMP(2.0) Delegates (built-in): bzlib cairo freetype gslib heic jng jp2 jpeg jxl lcms lqr lzma openexr pangocairo png ps raqm raw rsvg tiff webp xml zip zlib Compiler: Visual Studio 2022 (193532217)
To improve internet download speeds, some images may have been automatically converted (by ImageMagick, of course) from PNG or TIFF or MIFF to JPG.
Source file for this web page is gblevel.h1. To re-create this web page, execute "procH1 gblevel".
This page, including the images, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.
Anyone is permitted to re-publish this page, but only for non-commercial use.
Anyone is permitted to link to this page, including for commercial use.
Page version v1.0 15-August-2020.
Page created 23-Oct-2023 15:22:56.
Copyright © 2023 Alan Gibson.