snibgo's ImageMagick pages
Colours to matrix and polynomials
What -color-matrix or -function Polynomial will make one image look like another?
When we have two same-sized images with corresponding pixels, so there is a colour transformation but no geometric transformation, we can calculate the parameters for "-color-matrix" or "-function Polynomial" that approximate the transformation.
The method assumes the transformation is global rather than local, eg the entire image has been shifted towards red, rather than one part shifted towards red and another part towards blue.
Other methods for transforming images include:
Methods on this pages are generalisations of "gain and bias".
Scripts on this page assume that the version of ImageMagick in %IM7DEV% has been built with various process modules. See
Process modules.
IM's "-color-matrix" and "-function Polynomial" operations have mathematical definitions: each channel of each output pixel is calculated from a formula that has the channels of the corresponding input pixel and a list of numbers. We use these operations by supplying the list of numbers, so IM can calculate the output pixels.
This method operates the reverse process: given the input and output pixels, it calculates the list of numbers.
How does it do this? There is one equation per channel per pixel, with known channel values and unknown numbers in the list, but we know the same numbers are used in all the equations. So we have a bunch of simultaneous equations that can be solved for all the unknowns, which gives us the list of numbers. We often have more equations than unknowns, so we find the unknowns that minimizes the sum-of-squared-errors.
Why do we want this? We might have a set of input images that we want to normalise to a common standard. For example, time-lapse photos of a building site that we want to make into a movie. Or aerial photos that we want to join together. Or photos of an object taken under different lighting conditions. The same matrix or polynomial is then applied to any image for which we want the same transformation.
Before giving the method details, we will play with IM's colour matrix and polynomial to see how they work.
The following descriptions assume the three colour channels are RGB, but they could be Lab or YIQ or any other three-channel colorspace.
IM's operation "-color-matrix" calculates new pixels as the sum of a DC offset plus the colour components each multiplied by a factor. Hence, it provides for cross-feed between channels.
For RGB with offsets, we use a 6x6 matrix. The six columns and rows are the five channels (R, G, B, K, A) and an offset. "K" is the black channel of CMYK, and we don't use this. The top three rows specify the red, green and blue outputs. The bottom three rows are constant, and we don't usually want to change colours according to alpha, or to change alpha according to colours, so we have only 12 important values:
a,b,c,0,0,d,
e,f,g,0,0,h,
i,j,k,0,0,m,
0,0,0,1,0,0,
0,0,0,0,1,0,
0,0,0,0,0,1
(For clarity, I don't use the letter "L".)
When we know the values of a..m, each output R',G',B' is then calculated from the corresponding input R,G,B:
R' = R*a + G*b + B*c + d
G' = R*e + G*f + B*g + h
B' = R*i + G*j + B*k + m
A' = A
If we use only the diagonal elements a,f,k and the offsets d,h,m, setting other values to zero, we have the equivalent of the
gain and bias method, where a,f,k are the gain multipliers and d,h,m are the bias offsets.
Examples:
|
Identity matrix.
%IMG7%magick ^
toes.png ^
-color-matrix ^
1,0,0,0,0,0,^
0,1,0,0,0,0,^
0,0,1,0,0,0,^
0,0,0,1,0,0,^
0,0,0,0,1,0,^
0,0,0,0,0,1 ^
c2mp_cm1.png
|

|
|
Swap red and green channels.
%IMG7%magick ^
toes.png ^
-color-matrix ^
0,1,0,0,0,0,^
1,0,0,0,0,0,^
0,0,1,0,0,0,^
0,0,0,1,0,0,^
0,0,0,0,1,0,^
0,0,0,0,0,1 ^
c2mp_cm2.png
|

|
%IMG7%magick ^
toes.png ^
-color-matrix ^
1,0.25,0,0,0,-0.25,^
0,1,0,0,0,0,^
0,0,1,0,0,0,^
0,0,0,1,0,0,^
0,0,0,0,1,0,^
0,0,0,0,0,1 ^
c2mp_cm3.png
|

|
%IMG7%magick ^
toes.png ^
-color-matrix ^
1.1,0.25,0,0,0,-0.1,^
0.1,1,0.1,0,0,-0.2,^
-0.1,0,1,0,0,0,^
0,0,0,1,0,0,^
0,0,0,0,1,0,^
0,0,0,0,0,1 ^
c2mp_cm4.png
|

|
How do we get the 12 numbers a..m from two images? If the images each have N pixels, then we have N input values for each of R, G and B, and N output values for each of R', G' and B'. This gives us 3*N simultaneous equations that can be solved by Gauss-Jordan elimination.
For example, suppose an input pixel is RGB=(10%,20%,30%) and the corresponding output pixel is R'G'B'=(21%,22%,14%). This gives us three equations:
21 = 10*a + 20*b + 30*c + d
22 = 10*e + 20*f + 30*g + h
14 = 10*i + 20*j + 30*k + m
For this pair of pixels, the terms are (10,20,30,1), and the results are (21,22,14).
Four pairs of pixels would supply 12 simultaneous equations, so we could solve for the 12 unknowns a..m. If we have more than four pixels, the problem is over-determined and there may be no exact solution. But we can find a solution that minimizes the squared errors.
The output in each channel depends on the input in every channel, so we can't represent the transformation by simple "in versus out" curves.
We may wish to prevent the solution from cross-feeding between channels. The solution then has only six important values, gain a,f,k and bias d,h,m:
a,0,0,0,0,d,
0,f,0,0,0,h,
0,0,k,0,0,m,
0,0,0,1,0,0,
0,0,0,0,1,0,
0,0,0,0,0,1
The equations are:
R' = R*a + d
G' = G*f + h
B' = B*k + m
A' = A
The equations are fully independent; they have no elements in common. Hence they are solved as three independent problems.
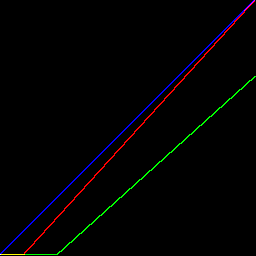
This is simple linear regression. The output in each channel depends on the input of that channel only, so we can represent the transformation by three simple curves (which are all straight lines):
set sMAT=^
1.1,0,0,0,0,-0.1,^
0,0.9,0,0,0,-0.2,^
0,0,1,0,0,0,^
0,0,0,1,0,0,^
0,0,0,0,1,0,^
0,0,0,0,0,1
%IMG7%magick ^
toes.png ^
-color-matrix %sMAT% ^
c2mp_cm4.png
%IMG7%magick ^
-size 1x256 gradient: -rotate 90 ^
-color-matrix %sMAT% ^
c2mp_cmgr4.png
call %PICTBAT%graphLineCol ^
c2mp_cmgr4.png . . 0
|

|
Constraining to just the gain can be useful. The solution then has only three important values, a,d,f:
a,0,0,0,0,0,
0,f,0,0,0,0,
0,0,k,0,0,0,
0,0,0,1,0,0,
0,0,0,0,1,0,
0,0,0,0,0,1
The equations are:
R' = R*a
G' = G*f
B' = B*k
A' = A
Again, the equations are fully independent, so they are solved as three independent problems.
A bias-only method is also possible, but doesn't seem useful.
IM's operation -function polynomial is closely related to -colour-matrix. We can apply a different polynomial to each channel, and that is how we will use it. There is no cross-channel mixing. Each output channel value is the sum of the input raised to a number of integer powers, each multipled by a coefficient.
If u is the input value normalised to typically between 0.0 to 1.0, and the polynomial is degree n, then the output u' is...
u' = an*un + an-1*un-1 + ... + a1*u + a0
Given a number of inputs u and corresponding outputs u', the module calculates the coefficients a0 ... an. The number of terms, and number of coefficients, is (n+1). We have one set of coefficients per channel, for a total of 3*(n+1) coefficients.
A polynomial of degree zero adds a constant value (a bias-only operation). A polynomial of degree one multiplies, then adds a constant value (a linear polynomial; a gain and bias operation). Polynomials of degree two are called quadratic; of degree three are called cubic. Higher degrees describe more complex transfer curves. A polynomial degree n can be used to transform an image of n pixels to any other image.
For example:
|
Set R' = -0.3*R2 + 0.8*R + 0.2, etc.
set sPOLY=^
-channel R -function Polynomial -0.3,0.8,0.2 ^
-channel G -function Polynomial 0.8,-0.1 ^
-channel B -function Polynomial 0.4
%IMG7%magick ^
toes.png ^
%sPOLY% ^
+channel ^
c2mp_pol1.png
|

|
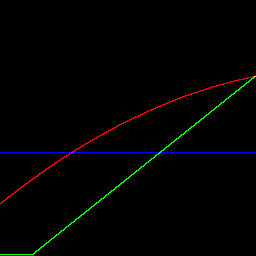
By applying the same operations to a gradient, we can get a transfer curve for each channel.
|
Set R' = -0.3*R2 + 0.8*R + 0.2, etc.
%IMG7%magick ^
-size 1x256 gradient: -rotate 90 ^
%sPOLY% ^
+channel ^
c2mp_polgr1.png
call %PICTBAT%graphLineCol ^
c2mp_polgr1.png . . 0
|
|
So, we can create a polynomial for each channel, and tweak a photo so its colour patches roughly match those of a reference. Higher degrees of polynomials will match the patches more closely, until perfection when the degree equals the number of patches. But this comes at a price: with higher degrees, the curve becomes increasingly eratic at colours other than the patches. In practice, degrees above three do not seem useful, and degree two is often sufficient.
set imgA=toes.png
|

|
set imgB=toes_x.jpg
|

|
When we have two same-sized images, "-process cols2mat" calculates the 12 numbers a..m and hence the 6x6 colour matrix, or the polynomial of required degree, that best transforms the first image to the second.
| Option |
Description |
Short
form |
Long form |
| m string
|
method string
|
Method for calculating the matrix, one of:
Cross include cross-channel multipliers (12 terms);
NoCross exclude cross-channel multipliers (6 terms);
NoCrossPoly polynomial without cross-channel (3*degreePoly+3 terms);
GainOnly include only this-channel multipliers (3 terms).
Default = Cross. |
| d integer
|
degreePoly integer
|
For method NoCrossPoly, degree of polynomial.
For example: degree 3 gives v' = a*v3 + b*v2 + c*v + d.
Default: 2. |
| w number
|
weightLast number
|
Weight for last line of image.
For example: more than 1.0 (eg 10, 100) to give greater weight to last line,
between 0.0 and 1.0 to give less weight.
Default: 1.0. |
| wa
|
weightAlpha
|
Multiplies weight by product of the pixel alphas. |
| x
|
noTrans
|
Don't replace images with transformation. |
| f string
|
file string
|
Write text data (the colour matrix) to stderr or stdout.
Default = stderr. |
| v
|
verbose
|
Write some text output to stderr. |
|
|
version
|
Write version information to stdout. |
The module needs two or three input images. The first two inputs must be the same size as each other. It replaces all the inputs with a single output image. It calculates the colour matrix or polynomial from the first two inputs. If there are only two inputs, the output is the first transformed by the colour matrix or polynomial. If there are three inputs then the output is the third transformed by the colour matrix or polynomial.
For the weightAlpha option, see
Weighting by alpha below.
The noTrans option will leave the image list unchanged. For applications that don't need a transformed image, it saves some time.
The inputs must have three colour chanels, representing RGB, L*a*b*, YIQ or whatever. For RGB images, I use it with sRGB colorspace, but I expect it will work with any profiled 3-channel colorspace.
Typically the first two inputs are small, for example 6x4 pixels. But they can be any size, provided they are the same size and the pixels correspond. It takes about four seconds to process a pair of 35 MP images.
For the NoCrossPoly method, the text output is three lists of polynomial coefficients. For the other methods, the text output is a single list of numbers in the 6x6 matrix. (A more general polynomial with cross-channel terms is possible, but IM has no operation for this.)
By default the calculation gives equal weight to all the input pixels, but a different weight may be applied to the last row on input pixels, and the weight may be multiplied by the product of the alphas.
The calculated 6x6 color matrix is sent as text to stderr or stdout, in a line that starts with "c2matrix=". The 36 numbers are separated by commas, with no spaces.
For example:
%IM7DEV%magick ^
%imgA% ^
%imgB% ^
-precision 9 ^
-process 'cols2mat f stdout' ^
c2mp_m1.png
|

|
c2matrix=1.8136873,-0.417894393,0.374689493,0,0,-0.362733056,-0.0860060676,1.72129904,-0.0694160492,0,0,-0.231379744,0.173499106,-0.19861703,1.69508299,0,0,-0.378856359,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
Warning: may clip Red shadows
Warning: may clip Red highlights
Warning: may clip Green shadows
Warning: may clip Green highlights
We can put the matrix into an environment variable like this:
set mymatrix=
for /F "usebackq tokens=1,2 delims==" %%A in (`%IM7DEV%magick ^
%imgA% ^
%imgB% ^
-precision 9 ^
-process 'cols2mat noTrans f stdout' ^
NULL:`) do (
if "%%A"=="c2matrix" set mymatrix=%%B
)
if "%mymatrix%"=="" goto error
echo mymatrix=%mymatrix%
mymatrix=1.8136873,-0.417894393,0.374689493,0,0,-0.362733056,-0.0860060676,1.72129904,-0.0694160492,0,0,-0.231379744,0.173499106,-0.19861703,1.69508299,0,0,-0.378856359,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
For example:
%IM7DEV%magick ^
%imgA% ^
%imgB% ^
-precision 9 ^
-process 'cols2mat method NoCrossPoly f stdout' ^
c2mp_p1.png
|

|
PolyRed=-2.10505152,4.19656686,-1.00894437
Warning: may clip Red shadows
Warning: may clip Red highlights
PolyGreen=-0.343882818,1.89691195,-0.305446549
Warning: may clip Green shadows
Warning: may clip Green highlights
PolyBlue=0.459346856,1.27933004,-0.298628025
Warning: may clip Blue shadows
Warning: may clip Blue highlights
We can put the polynomial coefficients into environment variables like this:
set mypolyr=
for /F "usebackq tokens=1,2 delims==" %%A in (`%IM7DEV%magick ^
%imgA% ^
%imgB% ^
-precision 9 ^
-process 'cols2mat method NoCrossPoly noTrans f stdout' ^
NULL:`) do (
if "%%A"=="PolyRed" set mypolyr=%%B
if "%%A"=="PolyGreen" set mypolyg=%%B
if "%%A"=="PolyBlue" set mypolyb=%%B
)
if "%mypolyr%"=="" goto error
echo mypolyr=%mypolyr%
echo mypolyg=%mypolyg%
echo mypolyb=%mypolyb%
mypolyr=-2.10505152,4.19656686,-1.00894437
mypolyg=-0.343882818,1.89691195,-0.305446549
mypolyb=0.459346856,1.27933004,-0.298628025
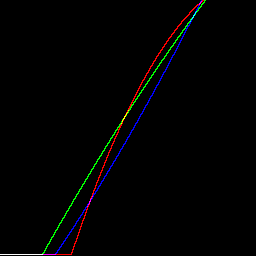
We can show the polynomials on a graph:
%IMG7%magick ^
-size 1x256 gradient: -rotate 90 ^
-channel R -function Polynomial %mypolyr% ^
-channel G -function Polynomial %mypolyg% ^
-channel B -function Polynomial %mypolyb% ^
+channel ^
c2mp_polygr.png
call %PICTBAT%graphLineCol ^
c2mp_polygr.png . . 0
|
|
We test a round trip: now we know the matrix that most closely transforms imgA to imgB, we can apply the matrix to imgA and the result should be close to imgB.
%IMG7%magick ^
%imgA% ^
-color-matrix %mymatrix% ^
%imgB% ^
-metric RMSE ^
-format %%[distortion] ^
-compare ^
info:
0.0632554
We also test a case where the inputs are equal. This should create the identity matrix, which has one in the diagonal elements and zero elsewhere.
%IM7DEV%magick ^
%imgA% ^
( +clone ) ^
-process 'cols2mat noTrans f stdout' ^
NULL:
c2matrix=1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
Another test, where each component is multiplied and added to:
%IM7DEV%magick ^
%imgA% ^
( +clone -evaluate Multiply 0.95 -evaluate Add 10%% ) ^
-process 'cols2mat noTrans f stdout' ^
NULL:
c2matrix=0.95,6.0394223e-13,2.6113502e-12,0,0,0.1,-5.4439919e-14,0.95,2.5774529e-12,0,0,0.1,1.1124435e-12,1.6980861e-13,0.95,0,0,0.1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
Warning: may clip Red highlights
Warning: may clip Green highlights
Limited arithmetic precision has prevented the cross-channel multipliers from being exactly zero. "method NoCross" will calculate the solution with zeros in those positions.
%IM7DEV%magick ^
%imgA% ^
( +clone -evaluate Multiply 0.95 -evaluate Add 10%% ) ^
-process 'cols2mat method NoCross noTrans f stdout' ^
NULL:
c2matrix=0.95,0,0,0,0,0.1,0,0.95,0,0,0,0.1,0,0,0.95,0,0,0.1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
Warning: may clip Red highlights
Warning: may clip Green highlights
For some cases, the module will not find a unique solution, usually because the problem is under-constrained (there are fewer simultaneous equations than unknowns). For example:
%IM7DEV%magick ^
xc:Red ^
xc:Blue ^
-process 'cols2mat noTrans f stdout' ^
NULL:
cols2mat: no solution found
No output line starts with "c2matrix=". Scripts should check for this condition.
(In fact, two solutions are possible: the blue output is the red input multiplied by one, or the blue output is set to an offset of one. Each of these solutions has an infinite number of variations.)
What matrix will make a larger image entirely blue?
%IM7DEV%magick ^
%imgA% ^
( +clone -fill Blue -colorize 100 ) ^
-process 'cols2mat noTrans f stdout' ^
NULL:
c2matrix=0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
A single solution is found: the blue output is set to an offset of one, with no channel multipliers.
We test a round trip: now we know the polynomials that most closely transforms c2mp_ph1_mat.png to c2mp_ph4_mat.png, we can apply them to c2mp_ph1_mat.png and the result should be close to c2mp_ph4_mat.png.
%IMG7%magick ^
%imgA% ^
-channel R -function Polynomial %mypolyr% ^
-channel G -function Polynomial %mypolyg% ^
-channel B -function Polynomial %mypolyb% ^
+channel ^
%imgB% ^
-metric RMSE ^
-format %%[distortion] ^
-compare ^
info:
0.0477719
We also test a case where the inputs are equal. This should create polynomials with one in the v1 elements and zero elsewhere.
%IM7DEV%magick ^
%imgA% ^
( +clone ) ^
-process 'cols2mat method NoCrossPoly d 1 noTrans f stdout' ^
NULL:
PolyRed=1,0
PolyGreen=1,0
PolyBlue=1,0
%IM7DEV%magick ^
%imgA% ^
( +clone ) ^
-process 'cols2mat method NoCrossPoly d 2 noTrans f stdout' ^
NULL:
PolyRed=1.110223e-16,1,5.5511151e-17
PolyGreen=0,1,0
PolyBlue=0,1,0
%IM7DEV%magick ^
%imgA% ^
( +clone ) ^
-process 'cols2mat method NoCrossPoly d 3 noTrans f stdout' ^
NULL:
PolyRed=-1.8605756e-15,3.3492796e-15,1,3.398451e-16
PolyGreen=0,0,1,0
PolyBlue=0,0,1,0
As before, a unique solution may not be found:
%IM7DEV%magick ^
xc:Red ^
xc:Blue ^
-process 'cols2mat method NoCrossPoly noTrans f stdout' ^
NULL:
cols2mat: no solution found
No output line starts with "PolyRed=" etc. Scripts should check for this condition.
What polynomials will make a larger image entirely blue?
%IM7DEV%magick ^
%imgA% ^
( +clone -fill Blue -colorize 100 ) ^
-process 'cols2mat method NoCrossPoly noTrans f stdout' ^
NULL:
PolyRed=0,0,0
PolyGreen=0,0,0
PolyBlue=0,0,1
A single solution is found: the blue output is set to an offset of one, with no channel multipliers.
The weightAlpha option calculates the solution of the simultaneous equations weighted by the product of the alphas of the input and output pixels. So if either pixel is entirely transparent, that pixel will be disregarded for the purpose of calculating the matrix or polynomial.
(Note that weightAlpha doesn't assume that pixel colours are calculated from alpha, nor that alpha is calculated. That would treat alpha like the colour channels, and I haven't included that in the module. I might in the future.)
|
toes_holed.png
|

|
|
Copy the hole to toes_x.jpg
%IMG7%magick ^
toes_x.jpg ^
toes_holed.png ^
-compose CopyOpacity -composite ^
-background Black -alpha Background ^
toes_x_holed.png
|

|
What colour matrix makes the grass of toes.png look like the grass of toes_x_holed.png?
%IM7DEV%magick ^
toes.png ^
toes_x_holed.png ^
-process 'cols2mat f stdout' ^
c2mp_th1.png
|

|
c2matrix=-0.62713194,1.9866906,-1.2680442,0,0,0.069961819,-1.4615194,2.9325759,-1.4897024,0,0,0.20511958,-0.65773008,1.1757757,-0.41449264,0,0,0.045947247,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
Warning: may clip Red highlights
Warning: may clip Green highlights
Oops. Most of toes_x_holed.png is (transparent) black, so the matrix is heavily influenced by this. We can eliminate the transparent pixels from the calculation by using the weightAlpha option:
%IM7DEV%magick ^
toes.png ^
toes_x_holed.png ^
-process 'cols2mat weightAlpha f stdout' ^
c2mp_th2.png
|

|
c2matrix=2.4829447,-0.13992561,0.063649543,0,0,-0.67242755,-0.12718404,1.6265641,0.10697504,0,0,-0.23135687,0.067065836,0.16431625,1.5729776,0,0,-0.46285413,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1
Warning: may clip Red shadows
Warning: may clip Red highlights
Warning: may clip Green shadows
Warning: may clip Green highlights
Even when both inputs are in the range 0 to 100%, the transformed output can be outside that range. If the image is saved to an integer format, values will be automatically clamped (aka clipped). If HDRI is used, pixels can be brought within gamut by "-clamp" or "-auto-level".
set FMT=^
red: %%[fx:minima.r] to %%[fx:maxima.r]\n^
green: %%[fx:minima.g] to %%[fx:maxima.g]\n^
blue: %%[fx:minima.b] to %%[fx:maxima.b]\n
%IM7DEV%magick ^
toes.png ^
toes_x_holed.png ^
-process 'cols2mat weightAlpha' ^
-format "%FMT%" ^
+write info: ^
c2mp_th3.png
red: -0.46074721 to 1.7434018
green: -0.14116973 to 1.2328533
blue: -0.42654275 to 1.2380592
|

|
%IM7DEV%magick ^
toes.png ^
toes_x_holed.png ^
-process 'cols2mat weightAlpha' ^
-auto-level ^
-format "%FMT%" ^
+write info: ^
c2mp_th4.png
red: 0 to 1
green: 0.14498906 to 0.76836933
blue: 0.015518218 to 0.77073119
|

|
As in the Wolf
reference, the module could be run for a pair of opaque inputs, then the difference between the output and second input is negated and used as the opacity for the first input of a re-run, and iterate until stability is reached. Thus outliers would count less towards a solution.
Polynomials with cross-channel terms could be created, eg:
R' = R2*d + G2*e + B2*f + R*G*g + G*B*h + B*R*i + R*a + G*b + B*c + j
IM has no built-in operator to process these, so that would also need to be written.
We could "regard alpha". This could calculate and use alpha in the same way as the colour channels.
We might have an option to save the colour matrix as a 6x6 image. Then another module can apply it to images. And another can do maths: concatenation.
Option to add zero and 100% for matrix calculation?
Can we use the Jump method to determine the best degree for polynomials?
All images on this page were created by the commands shown, using:
%IMG7%magick -version
Version: ImageMagick 7.1.0-42 Q16-HDRI x64 396d87c:20220709 https://imagemagick.org
Copyright: (C) 1999 ImageMagick Studio LLC
License: https://imagemagick.org/script/license.php
Features: Cipher DPC HDRI OpenCL
Delegates (built-in): bzlib cairo freetype gslib heic jng jp2 jpeg jxl lcms lqr lzma openexr pangocairo png ps raqm raw rsvg tiff webp xml zip zlib
Compiler: Visual Studio 2022 (193231332)
%IM7DEV%magick -version
Version: ImageMagick 7.1.0-20 Q32-HDRI x86_64 2021-12-29 https://imagemagick.org
Copyright: (C) 1999-2021 ImageMagick Studio LLC
License: https://imagemagick.org/script/license.php
Features: Cipher DPC HDRI Modules OpenMP(4.5)
Delegates (built-in): bzlib cairo fontconfig fpx freetype jbig jng jpeg lcms ltdl lzma pangocairo png raqm rsvg tiff webp wmf x xml zip zlib
Compiler: gcc (11.2)
Source file for this web page is col2mp.h1. To re-create this web page, execute "procH1 col2mp".
This page, including the images, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.
Anyone is permitted to re-publish this page, but only for non-commercial use.
Anyone is permitted to link to this page, including for commercial use.
Page version v1.1 9-Nov-2017.
Page created 04-Aug-2022 17:46:32.
Copyright © 2022 Alan Gibson.

















