Integral images

... for windowed mean and SD.

References
Sample input
IM's integral option
Process module: integim
Process module: deintegim
deintegim: dontdivide and adjedge
Extreme cases
Resampling the integral image
Comparison with "-statistic mean"
Performance
Application: windowed statistics
Application: thresholding
Application: detecting edges
Application: removing outliers
Application: sharpening
Application: generalized mean
Application: downsampling
Application: pyramids
Application: approximating other convolutions
Application: locating an approximate sub-image
How does it work?
Scripts

The Gradient contours page includes a scheme for 2D differentiation. The input image needs to be one channel (eg grayscale). The resulting differential needs two channels, for the slope in the x and y directions, so these are stored in output red and green channels. The differential at a pixel is the value at that pixel minus the pixel to the left or above. The inverse, for integrations, is also given, but this needs the top-left value to be known (the "DC offset").

The Slopes page shows a similar scheme for colour images, recording the x and y differences in a pair of images.

This page gives a different scheme for integration and differentiation. For both directions, each input channel needs only one output channel for storage, and each input pixel needs just one output pixel. Thus a colour input gives a colour output at the same size. No other data, such as a DC offset, need be recorded. However, calculations and data storage need to be HDRI.

The method is called integral images or summed area tables ("SAT") or running sums.

The modules should be compiled in a high-precision HDRI version of IM.

Scripts on this page assume that the version of ImageMagick in %IMDEV% has been built with various process modules (see Process modules), and is HDRI.

References

This page was inspired by:

Adaptive Thresholding Using the Integral Image Derek Bradley, Gerhard Roth, 2007

Sample input

set SRC=toes.png

This image is mostly transparent.

set SRC_TR=toes_holed.png

toes_holes.png has binary transparency. For demonstration purposes, we make a version with tapered transparency:

%IMG7%magick ^
  %SRC_TR% ^
  -alpha extract ^
  -blur 0x3 ^
  %SRC% ^
  +swap ^
  -alpha off ^
  -compose CopyOpacity -composite ^
  -background Black -alpha Background ^
  toes_holetap.png

set SRC_TT=toes_holetap.png

IM's integral option

Since this page was created, ImageMagick acquired an "-integral" option.

This creates an output the same size as the input, where values of each output pixel are set to the sum (aka integration) of input pixels above and to the left, including the input pixel at this location. The integration is applied only to selected channels, so the operation is sensitive to the -channel setting, but alpha is never integrated, and colour channel values are not multiplied by alph.

%IMG7%magick ^
  xc:sRGBa(10%,20%,30%,0.4) ^
  xc:sRGBa(71%,82%,93%,0.5) ^
  +append +repage ^
  -integral ^
  txt:

# ImageMagick pixel enumeration: 2,1,0,65535,srgba
0,0: (2570,7710,103,65535)  #0A0A1E1E0067FFFF  srgba(3.92157%,11.7647%,0.156863%,1)
1,0: (20817,31611,231,65535)  #51517B7B00E7FFFF  srgba(31.7647%,48.2353%,0.352941%,1)

Values in integral images generally exceed 100%, so HDRI must be used.

For a visual example, we show the integral image, which visually is almost entirely white, and then the result from "-auto-level".

%IMG7%magick ^
  %SRC% ^
  -integral ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  +write ii_im_ii1.miff ^
  -auto-level ^
  ii_im_ii1_al.png

IM does not include an operator for deintegration. But we can deintegrate with a 9x9 window like this:

%IMG7%magick ^
  ii_im_ii1.miff ^
  -fx "(p[5,5]-p[-4,5]-p[5,-4]+p[-4,-4])/81" ^
  ii_im_ii1_d.png

Note that a 9x9 window has a radius r of (9-1)/2=4, so we need offsets of -r = -4 and r+1 = +5, and we divide by the window area 9*9=81 to get the windowed mean.

The result is good except near the edges (boundaries) of the image. To fix that, we need a more sophisticated deintegration. The process module deintegim is explained below.

%IM7DEV%magick ^
  ii_im_ii1.miff ^
  -process 'deintegim window 9x9' ^
  ii_im_ii1_dae.png

We show integral and deintegration of an image with transparency:

%IMG7%magick ^ %SRC_TT% ^ -integral ^ -fx "(p[5,5]-p[-4,5]-p[5,-4]+p[-4,-4])/81" ^ ii_im_ii1_d2.png The result is almost entirely transparent.
Repeat, removing transparency: %IMG7%magick ^ %SRC_TT% ^ -integral ^ -fx "(p[5,5]-p[-4,5]-p[5,-4]+p[-4,-4])/81" ^ -alpha off ^ ii_im_ii1_d3.png Yuck.
We can save and restore alpha: %IMG7%magick ^ %SRC_TT% ^ ( +clone -alpha extract -write mpr:ALPH +delete ) ^ -integral ^ -fx "(p[5,5]-p[-4,5]-p[5,-4]+p[-4,-4])/81" ^ mpr:ALPH ^ -alpha off -compose CopyOpacity -composite ^ ii_im_ii1_d4.png Quite good, expect for the image edges.
Using `deintegral`: %IM7DEV%magick ^ %SRC_TT% ^ -integral ^ -alpha off ^ -process 'deintegim window 9x9' ^ ii_im_ii1_d5.png Quite good, expect for the semi-transparent input pixels.
Using `deintegral`, and save/restore alpha: %IM7DEV%magick ^ %SRC_TT% ^ ( +clone -alpha extract -write mpr:ALPH +delete ) ^ -alpha off ^ -integral ^ -evaluate Divide 81 ^ -process 'deintegim window 9x9 ae' ^ mpr:ALPH -alpha off -compose CopyOpacity -composite ^ ii_im_ii1_d6.png Visually good. However, the semi-transparent input pixels are incorrect.

Process module: integim

integim.c converts ordinary images into integral images (summed area tables).

Option		Description
Short form	Long form	Description
`pm` string	`premult` string	Whether to pre-multiply RGB values by alpha. One of: `yes` (do pre-multiply), `no` (don't pre-multiply), or `auto` (from current alpha setting). Default: `yes`.
`f` string	`file` string	Write verbose text to `stderr` or `stdout`. Default: `stderr`.
`v`	`verbose`	Write text information.

The result from integim is not particularly useful or interesting. Instead, the result is generally used by one or more calls to deintegim.

In this example we show the integral image, which visually is almost entirely white, then the result from "-auto-level".

%IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  +write ii_ii1.miff ^
  -auto-level ^
  ii_ii1_al.png

Process module: deintegim

deintegim.c converts from integral images (summed area tables) into ordinary images. It gives us, very quickly, the windowed mean of the image that was the input to integim.

Option		Description
Short form	Long form	Description
`w` string	`window` string	The window size, two numbers separated by "`x`". Each number may be suffixed with "`%`" or "`c`" or "`p`". Default: `1x1`.
`pd` string	`postdiv` string	Whether to post-divide RGB values by alpha. One of: `yes` (do post-divide), `no` (don't post-divide), or `auto` (from current alpha setting). Default: `yes`.
`ox` integer	`offsetX` integer	Offset for window centre in X-direction. Default: `0`.
`oy` integer	`offsetY` integer	Offset for window centre in Y-direction. Default: `0`.
`ae`	`adjedges`	Adjust divisor near image edges (boundaries).
`dd`	`dontdivide`	Don't divide colour channels by anything.
`f` string	`file` string	Write verbose text to `stderr` or `stdout`. Default: `stderr`.
`v`	`verbose`	Write text information.

The windows width and height are integers from one upwards. When the window size is 1x1, this is the inverse process to integim.

If the window option is not given, the window size will be 1x1. If the option is given, then both width and height must be given. Window dimensions are integers, from one upwards. If either dimension is in units of pixels (no suffix), it must be at least one.

A suffix may be used, to calculate the window dimension as a percentage or proportion of the image dimension. A suffix applies only to that dimension. For an image 3000x2000 pixels, the following window dimensions are equivalent:

300x100
10%x100
10cx100
0.1px100
10%x5%

If either dimension is calculated (because it has a suffix), the module will round to the nearest integer and ensure it is at least one.

When alpha is available, by default integim pre-multiplies colour channel by alpha, and deintegim post-divides by alpha. I think this is always desirable, but we can turn it off if we want (improving performance very slightly) or make this dependent on the image's -alpha setting.

If the input to deintegim is an ordinary image, not an integral image, we don't want to divide the colour channels by anything. That's what the dontdivide option is for.

dontdivide is also useful when we want a sum instead of a mean of the input to integim. However, the deintegration window shrinks as we approach an edge of the image, so the sum from dontdivide also decreases.

The option adjEdges adjusts for this, multiplying output pixel values by requested_window_area / actual_window_area. See below dontdivide and adjedge below.

The options adjEdges and dontdivide are mutually exclusive.

We de-integrate the result from integim:

Default window, 1x1.

%IM7DEV%magick ^
  ii_ii1.miff ^
  -process 'deintegim' ^
  ii_ii1_di.png

This should be an accurate reconstruction of %SRC%. Is it?

%IMG7%magick compare -metric RMSE %SRC% ii_ii1_di.png NULL:

32.8536 (0.000501314)

It is accurate, so the round trip integ-deinteg works.

The round trip in the other direction should also work:

Default window, 1x1.

%IM7DEV%magick ^
  %SRC% ^
  -process 'deintegim' ^
  -process 'integim' ^
  ii_de_in.png

%IMG7%magick compare -metric RMSE %SRC% ii_de_in.png NULL:

0 (0)

It is accurate, so the round trip deinteg-integ works.

More usefully, deintegim with a larger window size gives the mean for that area, and this is a blur.

%IM7DEV%magick ^ ii_ii1.miff ^ -process 'deintegim window 11x11' ^ ii_ii1_di2.png
%IM7DEV%magick ^ ii_ii1.miff ^ -process 'deintegim window 101x101' ^ ii_ii1_di3.png
%IM7DEV%magick ^ ii_ii1.miff ^ -process 'deintegim window 101x1' ^ ii_ii1_di4.png
%IM7DEV%magick ^ ii_ii1.miff ^ -process 'deintegim window 1x101' ^ ii_ii1_di5.png

When the window size has a high aspect ratio, eg 101x1 or 1x101, the result is gradually less blurred towards the sides or top and bottom. This is due to the window size decreasing.

We can, and often do, use integim and deintegim in the same command, without saving the intermediate integral image. Saving and re-reading would often be a significant proportion of the overall time taken.

%IM7DEV%magick ^ %SRC% ^ -process 'integim' ^ -process 'deintegim window 25x25' ^ ii_t_di.png
%IM7DEV%magick ^ %SRC_TT% ^ -process 'integim' ^ -process 'deintegim window 25x25' ^ ii_th_di.png

With a bit of work, we get an angled blur. For example, 20 degrees anti-clockwise from vertical:

%IM7DEV%magick ^
  %SRC% ^
  -set option:WW %%w ^
  -set option:HH %%h ^
  -virtual-pixel edge ^
  +distort SRT 1,20 ^
  -process 'integim' ^
  -process 'deintegim window 1x101' ^
  -set option:distort:viewport "%%[WW]x%%[HH]+0+0" ^
  +distort SRT 1,-20 ^
  ii_rotbl.png

deintegim: dontdivide and adjedge

For "-process deintegim", virtual pixels have no good meaning. In normal usage, when a deintegim window would have one or more corners outside the image ("virtual"), the code shrinks the window so corners are all inside the image ("authentic). As we normally want the mean of the values in the window, the code divides the pixel sums by the sum of the alpha values, which for opaque images is the window size, which gives the mean.

But sometimes we want the sum of the window values, not the mean. The option dontdivide simply omits the division operation. The windows near the image edge are smaller than the requested size, so sums there are smaller than sums near the centre, so the result is darker near the edges.

We illustrate with an artificial example, dividing by 101 before integrating, then deintegrating with a window of 101 pixels. We add a gray border to make the effect clear.

%IM7DEV%magick ^
  %SRC% ^
  -evaluate Divide 101 ^
  -process integim ^
  -process 'deintegim window 101x1 dontdivide' ^
  -bordercolor gray(50%%) -border 10 ^
  ii_examp_dd.png

Instead of dontdivide, the option adjedges fixes the problem. Instead of just dividing by the actual window area, it also multiplies by the requested window area.

%IM7DEV%magick ^
  %SRC% ^
  -evaluate Divide 101 ^
  -process integim ^
  -process 'deintegim window 101x1 adjedges' ^
  -bordercolor gray(50%%) -border 10 ^
  ii_examp_ae.png

We repeat those tests with the image that contains varying transparency:

%IM7DEV%magick ^
  %SRC_TT% ^
  -evaluate Divide 101 ^
  -process integim ^
  -process 'deintegim window 101x1 dontdivide' ^
  -bordercolor gray(50%%) -border 10 ^
  ii_examp_tt_dd.png

Instead of dontdivide, the option adjedges fixes the problem. Instead of just dividing by the actual window area, it also multiplies by the requested window area.

%IM7DEV%magick ^
  %SRC_TT% ^
  -evaluate Divide 101 ^
  -process integim ^
  -process 'deintegim window 101x1 adjedges' ^
  -bordercolor gray(50%%) -border 10 ^
  ii_examp_tt_ae.png

Extreme cases

We consider a couple of extreme (or "edge") cases. The code doesn't explicity test for these; the results are simply as expected from the algorithm.

When the input image is 1x1, the integral is a copy of the image, and the deintegral is the same. For example:

%IM7DEV%magick ^
  -size 1x1 xc:rgb(10%%,20%%,30%%) ^
  -process 'integim' ^
  +write txt: ^
  -process 'deintegim' ^
  txt:

# ImageMagick pixel enumeration: 1,1,0,4294967295,srgb
0,0: (429496730,858993459,1288490189)  #1999999A333333334CCCCCCD  srgb(10%,20%,30%)
# ImageMagick pixel enumeration: 1,1,0,4294967295,srgb
0,0: (429496730,858993459,1288490189)  #1999999A333333334CCCCCCD  srgb(10%,20%,30%)

When a window is large enough that in any position it will always cover the entire image (which happens when the window is at least twice the image dimensions), the output of deintegim will be a flat colour, which is the same value as "-scale 1x1!". For example:

%IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -process 'deintegim window 2px2p' ^
  +write ii_extr2.png ^
  -unique-colors ^
  txt:

The colour is:

# ImageMagick pixel enumeration: 1,1,0,65535,srgb
0,0: (34962,31843,29169)  #88927C6371F1  srgb(53.3492%,48.59%,44.5094%)

Compare this to the colour from -scale:

%IM7DEV%magick ^
  %SRC% ^
  -scale "1x1^!" ^
  txt:

# ImageMagick pixel enumeration: 1,1,0,65535,srgb
0,0: (34962,31843,29169)  #88927C6371F1  srgb(53.3492%,48.59%,44.5094%)

As expected, they are the same.

Resampling the integral image

If we subsample the integral image (resize it down), we should usually also divide the values by the ratio of the areas.

%IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -resize 50%% ^
  -evaluate Divide 4 ^
  -process 'deintegim' ^
  ii_subsamp1.png

%IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -resize 25%% ^
  -evaluate Divide 16 ^
  -process 'deintegim' ^
  ii_subsamp2.png

Similarly for supersampling, we multiply:

%IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -resize 200%% ^
  -evaluate Multiply 4 ^
  -process 'deintegim' ^
  ii_supsamp1.png

The edge colours are wrong, because "-resize" doesn't have a virtual-pixel method "continue changing values in the same direction".

Comparison with "`-statistic mean`"

For opaque images, the process modules and "-statistic mean" give similar results.

%IMG7%magick ^ %SRC% ^ -statistic mean 15x10 ^ ii_smc1.png
%IM7DEV%magick ^ %SRC% ^ -process 'integim' ^ -process 'deintegim window 15x10' ^ ii_smcp1.png

"-statistic mean" doesn't retain alpha, even when we use -alpha on ...

%IMG7%magick ^
  toes_holed.png ^
  -alpha on ^
  -statistic mean 15x15 ^
  ii_sm1.png

... so we can save the alpha and restore it afterwards, or use "-channel RGBA". But, because "-statistic mean" doesn't ignore transparent pixels, the transparent black leaks into the rest of the image. This is most obvious when we flatten against a gray background.

%IMG7%magick ^ toes_holed.png ^ ( +clone ^ -alpha extract ^ +write mpr:ALPH ^ +delete ^ ) ^ -statistic mean 15x15 ^ mpr:ALPH ^ -alpha off -compose CopyOpacity -composite ^ ii_sm2.png The boundary is darkened.
Apply "-statistic mean" to the extracted alpha: %IMG7%magick ^ toes_holed.png ^ ( +clone ^ -alpha extract ^ -statistic mean 15x15 ^ +write mpr:ALPH ^ +delete ^ ) ^ -statistic mean 15x15 ^ mpr:ALPH ^ -alpha off ^ -compose CopyOpacity -composite ^ -compose Over ^ +write ii_sm3.png ^ -background gray(50%%) ^ -layers Flatten ^ ii_sm3g.png The semi-transparent area is darkened.
Apply "-statistic mean" to the four channels: %IMG7%magick ^ toes_holed.png ^ -channel RGBA ^ -statistic mean 15x15 ^ +channel ^ +write ii_sm3a.png ^ -background gray(50%%) ^ -layers Flatten ^ ii_sm3ag.png The semi-transparent area is darkened.
Using the process modules: %IM7DEV%magick ^ toes_holed.png ^ -process 'integim' ^ -process 'deintegim window 15x15' ^ ii_smpm3.png ^ -background gray(50%%) ^ -layers Flatten ^ ii_smpm3g.png There is no darkening.

Examples of thin kernels:

%IMG7%magick ^ %SRC% ^ -statistic mean 101x1 ^ ii_smt1.png Artificial sharpness at the edges of the blur.
Virtual pixel `Mirror` instead of `Edge`. %IMG7%magick ^ %SRC% ^ -virtual-pixel Mirror ^ -statistic mean 101x1 ^ ii_smt1b.png
%IM7DEV%magick ^ %SRC% ^ -process 'integim' ^ -process 'deintegim window 101x1' ^ ii_smtp1.png
%IMG7%magick ^ %SRC% ^ -virtual-pixel Mirror ^ -statistic mean 1x101 ^ ii_smt2.png
%IM7DEV%magick ^ %SRC% ^ -process 'integim' ^ -process 'deintegim window 1x101' ^ ii_smtp2.png

There is a difference at the edges. For example, "-statistics mean" has a sharpness at the left and right edges of the horizontal blur, whereas the modules have a more consistent blur from the center to the edges.

"-statistics mean" uses virtual pixels, which by default are "edge", so when we are working on the bottom row, with a 1x101 window, "-statistics mean" will use the bottom row 50 times out of the 101 window pixels, so this gives undue weight to the bottom row of pixels.

By contrast, deintegim doesn't use virtual pixels. When a window would overlap the edge of an image, the window size is reduced so it doesn't overlap. For example, with a 1x101 window centred at the image edge, it will cap the size of the window to 51 pixels high so the bottom row will contribute 1 out of the 50 window pixels.

The "-statistics mean" edge problem is reduced by using mirrored virtual pixels:

%IMG7%magick ^ %SRC% ^ -virtual-pixel Mirror ^ -statistic mean 101x1 ^ ii_smtm1.png
%IMG7%magick ^ %SRC% ^ -virtual-pixel Mirror ^ -statistic mean 1x101 ^ ii_smtm2.png

Comparing performance:

timec %IM7DEV%magick ^
  %SRC% ^
  -statistic mean 101x101 ^
  NULL:

 TimeC C:\cygwin64\home\Alan\imdevins71019fx3\bin\magick toes.png -statistic mean 101x101 NULL:
Seconds: 0.91

timec %IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -process 'deintegim window 101x101' ^
  NULL:

 TimeC C:\cygwin64\home\Alan\imdevins71019fx3\bin\magick toes.png -process 'integim' -process 'deintegim window 101x101' NULL:
Seconds: 0.37

The improvement is clear.

Performance

The time required for both integim and deintegim is proportional to the image size in pixels, and is independent of the window size. Both processes require just one pass through their inputs, so they are fast.

set LGE_IMG=AGA_1434_gms.tiff

%IMG7%magick identify %LGE_IMG%

AGA_1434_gms.tiff TIFF 4924x7378 4924x7378+0+0 16-bit sRGB 166.02MiB 0.002u 0:00.001

 %IM7DEV%magick ^
  %LGE_IMG% ^
  -process 'integim' ^
  -process 'deintegim window 501x501' ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_perf.miff

0 00:00:10

This time includes disk I/O.

Application: windowed statistics

We readily find windowed statistics.

The script iiMeanSd.bat creates the mean, or the standard deviation, or both.

call %PICTBAT%iiMeanSd ^
  %SRC% ^
  ii_scr_mn.miff ^
  ii_scr_sd.miff ^
  15x15

Mean

Each result pixel is the mean of input pixels within a window. The process modules give us this directly.

%IM7DEV%magick ^
  %SRC% ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_mn.miff

%IM7DEV%magick ^
  %SRC_TT% ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_tt_mn.miff

Local adaptive threshold

If a pixel value is lighter than the windowed mean plus an offset, it is made white. Otherwise, it is made black. For example, with a 15x15 window and 10% offset:

%IM7DEV%magick ^
  %SRC% ^
  ( +clone ^
    -process 'integim' ^
    -process 'deintegim window 15x15' ^
  ) ^
  -compose MinusSrc ^
  -composite ^
  -channel RGB ^
  -threshold 10%% ^
  +channel ^
  ii_ap_lat.miff

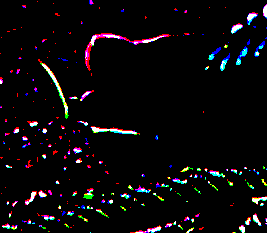
This is equivalent to "-lat", except near the edges because the process modules don't use virtual pixels:

%IM7DEV%magick ^
  %SRC% ^
  -lat 15x15+10%% ^
  ii_lat2.miff

Mean square

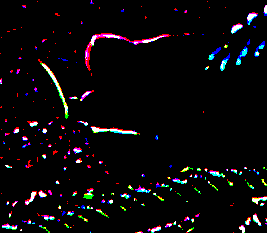
We square the input colour channels first, and find the mean of that.

%IM7DEV%magick ^
  %SRC% ^
  -channel RGB ^
  -evaluate Pow 2 ^
  +channel ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_ms.miff

%IM7DEV%magick ^
  %SRC_TT% ^
  -channel RGB ^
  -evaluate Pow 2 ^
  +channel ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_tt_ms.miff

Root mean square

We square the input, find the mean of that, and take the square root.

%IM7DEV%magick ^
  %SRC% ^
  -channel RGB ^
    -evaluate Pow 2 ^
  +channel ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  -channel RGB ^
    -evaluate Pow 0.5 ^
  +channel ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_rms.miff

%IM7DEV%magick ^
  %SRC_TT% ^
  -channel RGB ^
    -evaluate Pow 2 ^
  +channel ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  -channel RGB ^
    -evaluate Pow 0.5 ^
  +channel ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_tt_rms.miff

Standard deviation

SD = sqrt ( mean(image²) - imagemean² )

mean(image²) is the mean square image as calculated above, and imagemean is the mean of the image as also calculated above.

%IM7DEV%magick ^
  ii_ap_mn.miff ^
  -channel RGB ^
    -evaluate Pow 2 ^
  +channel ^
  ii_ap_ms.miff ^
  -define compose:clamp=off ^
  -compose MinusDst -composite ^
  -channel RGB ^
    -evaluate Pow 0.5 ^
  +channel ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_sd.miff

%IM7DEV%magick ^
  ii_ap_tt_mn.miff ^
  -channel RGB ^
    -evaluate Pow 2 ^
  +channel ^
  ii_ap_tt_ms.miff ^
  -define compose:clamp=off ^
  -compose MinusDst -composite ^
  -channel RGB ^
    -evaluate Pow 0.5 ^
  +channel ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_tt_sd.miff

Skew

We use the derivation:

skew = mean(diffmean³) / SD³

... where diffmean is the image minus its mean.

%IM7DEV%magick ^
  %SRC% ^
  ii_ap_mn.miff ^
  -define compose:clamp=off ^
  -compose MinusSrc -composite ^
  -channel RGB ^
    -evaluate Pow 3 ^
  +channel ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  ( ii_ap_sd.miff ^
    -channel RGB ^
      -evaluate Pow 3 ^
    +channel ^
  ) ^
  -compose DivideSrc -composite ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_sk.miff

Kurtosis

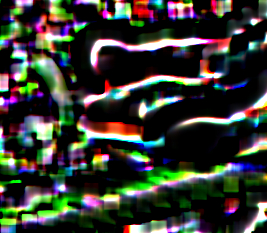
kurtosis = mean(diffmean⁴) / SD⁴

%IM7DEV%magick ^
  %SRC% ^
  ii_ap_mn.miff ^
  -define compose:clamp=off ^
  -compose MinusSrc -composite ^
  -channel RGB ^
    -evaluate Pow 4 ^
  +channel ^
  -process 'integim' ^
  -process 'deintegim window 15x15' ^
  ( ii_ap_sd.miff ^
    -channel RGB ^
      -evaluate Pow 4 ^
    +channel ^
  ) ^
  -compose DivideSrc -composite ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  ii_ap_kt.miff

Application: thresholding

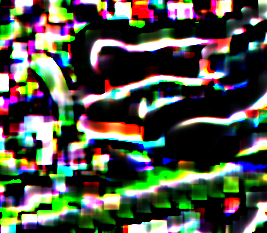
We use two examples from the Bradley and Roth paper. These images are not my copyright.

`bradley_0.png`
`bradley_1.png`

The method makes a windowed mean size s x s. If an input pixel is t percent less than this average the output is black, otherwise the output is white. For example, when t is 15%, we multiply the average by 0.85, and compare this to the input pixel. Bradley and Roth do not say what values they used for s and t to get their results.

set BRAD_S=12
set BRAD_T=0.85

%IM7DEV%magick ^
  bradley_0.png ^
  -colorspace Gray ^
  ( +clone ^
    -process 'integim' ^
    -process 'deintegim w %BRAD_S%x%BRAD_S%' ^
    -evaluate Multiply %BRAD_T% ^
  ) ^
  -define compose:clamp=off ^
  -compose MinusSrc -composite ^
  -define quantum:format=floating-point ^
  -threshold 0 ^
  ii_brad_0.png

set BRAD_S=65
set BRAD_T=0.85

%IM7DEV%magick ^
  bradley_1.png ^
  -colorspace Gray ^
  ( +clone ^
    -process 'integim' ^
    -process 'deintegim w %BRAD_S%x%BRAD_S%' ^
    -evaluate Multiply %BRAD_T% ^
  ) ^
  -define compose:clamp=off ^
  -compose MinusSrc -composite ^
  -define quantum:format=floating-point ^
  -threshold 0 ^
  ii_brad_1.png

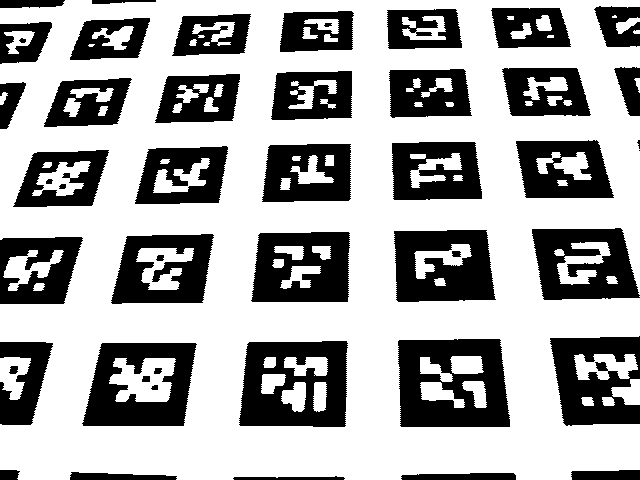
ASIDE: This thresholding method was designed to be very fast, for real-time video processing, rather than preparation for OCR.

Application: detecting edges

The deintegim module can be used alone, with an ordinary image as input. Each output pixel depends on only four input pixels, so this is fast but sensitive to noise. The output measures the slope between the four pixels, and may be positive or negative.

In the examples, we adjust the output to increase visibility.

%IM7DEV%magick ^
  %SRC% ^
  -process 'deintegim' ^
  -evaluate Multiply 4 ^
  -evaluate Add 50%% ^
  ii_edge1.png

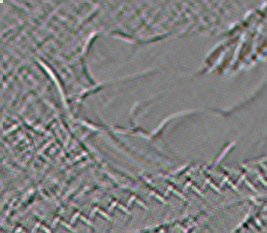
%IM7DEV%magick ^
  %SRC% ^
  -process 'deintegim window 5x5 dontdivide' ^
  -evaluate Add 50%% ^
  ii_edge2.png

Note that if we dontdivide and the input to deintegim ranges from 0 to 100%, its output range is -200% to +200%.

Application: removing outliers

For some purposes, we might define a local outlier as a pixel with value outside the range (mean ± k * SD) where the mean and standard deviation are for a window around the pixel, and k is a desired constant for the limit, typically between 1.0 and 3.0. We might replace outliers with the range limit, ie:

if      v > mean + k*SD then v' = mean + k*SD
else if v < mean - k*SD then v' = mean - k*SD
else                         v' = v

For ImageMagick, this is more conveniently expressed as:

v' = min (mean + k*SD, max (mean - k*SD, v))

We put this in a script, deOutlier.bat. In a single magick, the script calculates the windowed mean and SD (code copied from iiMeanSd.bat), then the maximum of the image and (mean-k*SD), then the minimum of that and (mean+k*SD), and limits each pixel value to fall within this minimum and maximum.

call %PICTBAT%deOutlier ^
  %SRC% ^
  ii_do1.jpg ^
  15x15 2

The effect is more obvious with small values for k:

call %PICTBAT%deOutlier ^
  %SRC% ^
  ii_do2.jpg ^
  15x15 0.5

The effect will generally move values inwards from 0 and 100%, so "-auto-level" may be beneficial:

call %PICTBAT%deOutlier ^
  %SRC% ^
  ii_do3.jpg ^
  15x15 0.5 ^
  -auto-level

Removing local outliers reduces "pep" or "zing", and increasing standard deviation can improve that in the mid-tones, at the expense of reducing contrast in the highlights and shadows. See Process modules: setmnsd.

call %PICTBAT%deOutlier ^
  %SRC% ^
  ii_do4.jpg ^
  15x15 0.5 ^
  "-auto-level -process 'setmnsd sd 0.2 direction incOnly'"

The process can be iterated:

%IMG7%magick %SRC% ii_tmp.miff

for /L %%I in (0,1,9) ^
do call %PICTBAT%deOutlier ^
  ii_tmp.miff ^
  ii_tmp.miff ^
  15x15 0.5 ^
  -auto-level

%IMG7%magick ii_tmp.miff ii_doiter.jpg

Removing outliers can be regarded as a noise-reduction method, or as a form of edge-preserving adaptive blur. It is similar to "-statistic median", which replaces each pixel by the median of the window. Note that for any set of numbers, the median is within the range mean plus or minus one standard deviation (inclusive):

mean-SD <= median <= mean+SD

This method could be extended so that k was not a constant, but varied across pixels, according to a colour or edge detector or some other mask.

Application: sharpening

We show two methods. They are both variations on sharpening by unsharp-mask, where we take an unsharp (ie blurred) image and extrapolate from that blur back to the source and beyond. This increases contrast in detail that was removed by the blur.

1. Sharpening by extrapolation from mean

We can use the mean directly as an unsharp mask:

%IM7DEV%magick ^
  %SRC% ^
  ( +clone ^
    -process 'integim' ^
    -process 'deintegim window 15x15' ^
  ) ^
  -compose Blend ^
    -define compose:args=-100 ^
    -composite ^
  ii_usm.png

2. Sharpening by extrapolation from removed outliers

Removing outliers will attenuate fine detail, while (roughly) preserving gradients and edges. It removes ("blurs") high frequencies. So extrapolating from that result back to the source and beyond will exagerate outliers, amplifying fine detail, leaving gradients and edges (roughly) unchanged. We don't use "-auto-level" after removing outliers because that would mess up the extrapolation. For example:

call %PICTBAT%deOutlier ^
  %SRC% ^
  ii_4shp.miff ^
  15x15 0.5

%IMG7%magick ^
  ii_4shp.miff %SRC% ^
  -compose Blend ^
    -define compose:args=250 ^
  -composite ^
  ii_shp.miff

Increasing sharpness by extrapolation can create clipping. To avoid that, we can use Process module: oogbox.

%IM7DEV%magick ^
  ii_4shp.miff %SRC% ^
  -compose Blend ^
    -define compose:args=250 ^
  -composite ^
  -process 'oogbox' ^
  ii_shp2.jpg

An alternative method for preventing clipping is to limit changes to the local minimum or maximum. (See Limit min-max.) This also prevents overshoot, so it reduces the sharpening effect.

call %PICTBAT%limitMinMax ^
  toes.png ^
  ii_shp.miff ^
  ii_shp3.jpg

Application: generalized mean

See Wikipedia: Generalized mean.

The ordinary arithmetic mean is:

M(x₁,...x_n) = sum(x_i)/n

The generalized mean is:

M_p(x₁,...x_n) = [sum(x_i^p)/n]^1/p

... where p is non-zero and x_i are positive. Some values for p yield special results:

p	Description
-∞	minimum
-1	harmonic mean
0	geometric mean
1	arithmetic mean
2	quadratic mean
3	cubic mean
+∞	maximum

We use the same window for sample results:

set INTEG=^
  -process 'integim' ^
  -process 'deintegim window 15x15'

sRGB		linear RGB
set p=-20 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gmminf.jpg		set p=-20 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gmminf_lin.jpg
set p=-1 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gmm1.jpg		set p=-1 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gmm1_lin.jpg
set p=0.01 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gmpz.jpg		set p=0.01 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gmpz_lin.jpg
set p=1 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gm1.jpg		set p=1 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gm1_lin.jpg
set p=2 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gm2.jpg		set p=2 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gm2_lin.jpg
set p=3 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gm3.jpg		set p=3 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gm3_lin.jpg
set p=20 %IM7DEV%magick ^ %SRC% ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ ii_gmpinf.jpg		set p=20 %IM7DEV%magick ^ %SRC% ^ -colorspace RGB ^ -evaluate Pow %p% ^ %INTEG% ^ -evaluate Pow ^ %%[fx:1/(%p%)] ^ -colorspace sRGB ^ ii_gmpinf_lin.jpg

Higher values of abs(p) create blockier results.

We can compare the first and last with correct versions of minimum and maximum:

%IMG7%magick ^
  %SRC% ^
  -statistic Minimum 15x15 ^
  ii_min.jpg

%IMG7%magick ^
  %SRC% ^
  -statistic Maximum 15x15 ^
  ii_max.jpg

Application: downsampling

deintegim could be modified to make the output smaller than the input. At each output pixel, calculate the required (x1,y1) and (x2,y2) window on the input, to calculate the output pixel as a present.

This would give a very fast downsampling method, though it may have little or no benefit over IM's -scale or -sample.

Application: pyramids

Multi-resolution pyramids could be constructed very quickly.

Application: approximating other convolutions

integim followed by deintegim is a box filter. Other filters can be approximated, to any desired accuracy, by a series of box filters of appropriate sizes and weights.

For example, the Stacked Integral Images (SII) method to approximate Gaussian filters can be implemented by a single run of integim followed by multiple runs of deintegim (or a single run of integim followed by a single run of a modified version of deintegim that has multiple look-ups). "Multiple" is a small number, eg 3, 4 or 5.

This is explored in Gaussian blur by integral images.

Application: locating an approximate sub-image

Suppose we have a large image L size W_LxH_L and a small image S size W_SxH_S, and we want to find the closest approximation to S in L. Examples include tracking the movement of an object in a video sequence, and searching an image for a texture.

One method is to make a histogram of S. This contains N bins representing N intensities or colour values, each bin with a count of the pixels that fall within the bin. N might be small, eg 16. Then make a histogram for each W_SxH_S sub-image of L, and find the distance between this and the histogram of S. The closest histogram tells us which sub-image is the closest. (The "distance between histograms" is a complex topic.)

But that would be a large number of histograms. Instead, we make N images each size W_LxH_L. Each contains the cumulative number of pixels that fall into that bin. So each is an integral image, and finding the histogram for any rectangle involves four lookups in each of the N images.

This is described in:

Integral Histogram: A Fast Way to Extract Histograms in Cartesian Spaces Fatih Porikli, 2005 .
Robust Fragments-based Tracking using the Integral Histogram Adam et al, 2006 .

How does it work?

Integral image

An integral (or summed area table) of an image has pixel values of each coordinate set to the sum of the image's pixel values across a rectangle from the origin (0,0) to this coordinate, inclusive. This is done for each channel. Processing, and the integral image itself, needs to be HDRI.

If f(x,y) is the input image then I(x,y) is the integral image, calculated as:

I(x,y) = f(x,y) + I(x-1,y) + I(x,y-1) - I(x-1,y-1).

When x<0 or y<0, I(x,y)==0.

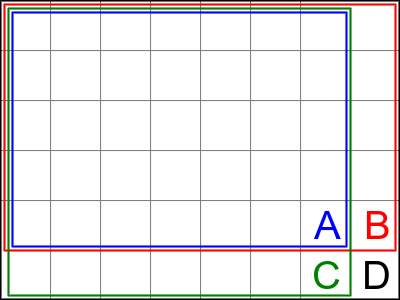
ASIDE: To see why this is true, consider this diagram, which represents a 8x6 pixel integral image.

Suppose A is the sum of all the input pixels in the 7x5 blue rectangle, B is the sum of all the input pixels in the 8x5 red rectangle, and C is the sum of all the input pixels in the 7x6 green rectangle.

We want to calculate D, the sum of all the input pixels in the black rectangle, which in this case is all the pixels.

By inspection, D equals the corresponding pixel from the input image, plus B plus C minus A.

Also, provided input pixels are positive: D>=C, D>=B, C>=A, B>=A.

So the top-left pixel of the integral will be a copy of the same pixel in the input image.

In words: the integral at a pixel is the value at that pixel, plus the integral to the left, plus the integral above, minus the integral above and left.

We can implement this using the more primitive process module cumulhisto in both directions. cumulhisto integrates in one direction only, from left to right, on each row separately. We take the output from this and rotate, then apply cumulhisto to that, and rotate back. The result is the required two-dimensional integral.

%IM7DEV%magick ^
  %SRC% ^
  -process 'cumulhisto' ^
  -rotate -90 ^
  -process 'cumulhisto' ^
  -rotate +90 ^
  +depth ^
  -define quantum:format=floating-point ^
  ii_integ.miff

%IM7DEV%magick ^
  ii_integ.miff ^
  info:

ii_integ.miff MIFF 267x233 267x233+0+0 32-bit TrueColor sRGB 747745B 0.079u 0:00.076

How does cumulhisto help us?

cumulhisto returns an image, where each ouput pixel is the sum of the corresponding pixel and all the pixels to its left on the same row:

C(x,y) = f(x,y) + C(x-1,y)

When used vertically:

C'(x,y) = f'(x,y) + C'(x,y-1)

We feed C() into f'(), so substitute:

C'(x,y) = f(x,y) + C(x-1,y) + C'(x,y-1)

In words: the integral at (x,y) is the input at (x,y) plus the input pixels to the left, plus the integral at (x,y-1). Which is what we want.

We put this in a script, integral.bat.

Here are some statistics of the integral image, as multiples of Quantum:

set FMT=^
minRed=%%[fx:minima.r] minGreen=%%[fx:minima.g] minBlue=%%[fx:minima.b]\n^
meanRed=%%[fx:mean.r] meanGreen=%%[fx:mean.g] meanBlue=%%[fx:mean.b]\n^
maxRed=%%[fx:maxima.r] maxGreen=%%[fx:maxima.g] maxBlue=%%[fx:maxima.b]\n

%IM7DEV%magick ^
  ii_integ.miff ^
  -format "%FMT%" ^
  info:

minRed=0.380148 minGreen=0.443153 minBlue=0.254185
meanRed=7837.37 meanGreen=7609.21 meanBlue=6580.77
maxRed=33189.1 maxGreen=30228.3 maxBlue=27689.8

As expected, values are a large multiple of Quantum.

-auto-level compresses the values to the range 0 to 100% of Quantum, so we can view the image, just for interest:

%IM7DEV%magick ^
  ii_integ.miff ^
  -auto-level ^
  ii_integ_al.png

In each channel, values increase monotonically from left to right and from top to bottom.

Differentiating

The inverse of integration is differentiation.

If f(x,y) is the input image and I(x,y) is the integral image, then:

f(x,y) = I(x,y) - I(x-1,y) - I(x,y-1) + I(x-1,y-1).

... where x<0 or y<0, I(x,y)==0.

In words: the differential at a pixel is set to the integral at that pixel, minus the integral to the left, minus the integral above, plus the integral above and left.

This is readily implemented as a command:

%IM7DEV%magick ^
  ii_integ.miff ^
  ( -clone 0 -repage +1+0 ) ^
  ( -clone 0 -repage +0+1 ) ^
  ( -clone 0 -repage +1+1 ) ^
  -virtual-pixel Black ^
  -background None ^
  -define compose:clamp=off ^
  ( -clone 0-1 ^
    -compose MinusSrc -layers Flatten ^
    -clone 3 ^
    -compose Plus -layers Flatten ^
    -clone 2 ^
    -compose MinusSrc -layers Flatten ^
    +repage ^
  ) ^
  -delete 0-3 ^
  -alpha off ^
  ii_diff.png

Or, far more simply:

%IM7DEV%magick ^
  ii_integ.miff ^
  -virtual-pixel Black ^
  -morphology convolve "2x2+0+0:1,-1,-1,1" ^
  ii_diff2.png

We put this in a script, deintegral.bat.

This should be an accurate reconstruction of %SRC%. Is it?

%IMG7%magick compare -metric RMSE %SRC% ii_diff.png NULL:

32.8536 (0.000501314)

It is accurate, so the round trip integrate-differentiate works.

Vice versa

We can process in the opposite direction: differentiate first, then integrate.

Differentiate:

call %PICTBAT%deintegral ^
  %SRC% ii_deint.miff

Make the differential more visible:

%IM7DEV%magick ^
  ii_deint.miff ^
  -evaluate Add 50%% ^
  -sigmoidal-contrast 5,50% ^
  -auto-level ^
  ii_deint_al.png

Integrate:

call %PICTBAT%integral ^
  ii_deint.miff ii_deint_int.png

How accurately does this reconstruct %SRC%?

%IMG7%magick compare -metric RMSE %SRC% ii_deint_int.png NULL:

27.1085 (0.000413649)

It is accurate.

De-integrating with windows

Okay, but what is the point of an integral image? It allows us to quickly calculate the sum (or mean) of the input image over a window of any size. The window width and height must both be integers, and usually odd numbers.

FUTURE: Non-integer window sizes could be handled, by deintegim interpolating the four pixels. This would be slower, and I can't see any need for this.

If the window is from (x₁,y₁) to (x₂,y₂) inclusive, then:

sum(x₁,y₁,x₂,y₂) = I(x₂,y₂) - I(x₂,y₁-1) - I(x₁-1,y₂) + I(x₁-1,y₁-1)

ASIDE: To see why this is, consider a rectangle divided into four areas A, B, C and D.

The top-left pixel of D is at (x₁,y₁), so the bottom-right pixel of A is at (x₁-1,y₁-1).

We can calculate the area of D:

D = (A+B+C+D)
  - (A+B)
  - (A+C)
  + (A)

This gives us the sum over a window. More often we want the mean over the window, so we divide by the number of pixels in the window:

winArea = (x₂-x₁)*(y₂-y₁)

mean(x₁,y₁,x₂,y₂) = (I(x₂,y₂) - I(x₂,y₁-1) - I(x₁-1,y₂) + I(x₁-1,y₁-1)) / winArea

set WINRAD=10
set /A WINRADp1=%WINRAD%+1
set /A WINAREA=(%WINRAD%*2+1)*(%WINRAD%*2+1)

%IM7DEV%magick ^
  ii_integ.miff ^
  ( -clone 0 -repage -%WINRAD%-%WINRAD% ) ^
  ( -clone 0 -repage -%WINRAD%+%WINRADp1% ) ^
  ( -clone 0 -repage +%WINRADp1%-%WINRAD% ) ^
  ( -clone 0 -repage +%WINRADp1%+%WINRADp1% ) ^
  -delete 0 ^
  -virtual-pixel Black ^
  -background None ^
  -define compose:clamp=off ^
  ( -clone 0-1 ^
    -compose MinusSrc -layers Merge ^
    -clone 3 ^
    -compose Plus -layers Merge ^
    -clone 2 ^
    -compose MinusSrc -layers Merge ^
    +repage ^
  ) ^
  -delete 0-3 ^
  -evaluate Divide %WINAREA% ^
  ii_mean.png

This is the same as the first de-integration command above, but with different offsets and a division at the end.

Pixels near the edge are a pain. The window is effectively smaller near the edges, so we might divide by another image that represented the variable window area. This is easy in C code (eg the deintegim process module) but is awkward in a CLI command.

In these scripts, we solve the edge problem by extending the edges of the input to the integral process on the left and right by the window width, and on top and bottom by the window height. Scripts take an argument of the window size, the width and height in pixels.

We put the above command in a script, integMean.bat. As input, this takes an integral image that has been made with extended edges. It creates a windowed mean as output, cropping off the extensions.

call %PICTBAT%integral ^
  %SRC% ii_integ2.miff 11x11

call %PICTBAT%integMean ^
  ii_integ2.miff ii_mean2.png 11x11

We compare this result with "-statistic mean 11x11".

%IMG7%magick ^
  %SRC% ^
  -statistic mean 11x11 ^
  ii_stmean.png

%IMG7%magick compare -metric RMSE ii_stmean.png ii_mean2.png NULL:

0.549613 (8.38655e-06)

They are virtually identical.

Another script, integMeanSd.bat, takes an ordinary image as input, and makes both mean and standard deviation outputs.

call %PICTBAT%integMeanSd ^
  %SRC% ii_mean3.png ii_sd3.png 11x11

We compare the results of integMean.bat and integMeanSd.bat.

%IMG7%magick compare -metric RMSE ii_mean2.png ii_mean3.png NULL:

0 (0)

They are virtually identical.

For more details in this topic, see the Windowed mean and standard deviation page.

Transparency

When an image has transparency, integim and deintegim calculate the alpha channel exactly as described above.

The colour channels are either also calculated as above, or integim pre-multiples by alpha and deintegim post-divides by alpha.

If a(x,y) is alpha in the input image and Ia(x,y) is the integral alpha, the pre-multiply formulae used by integim are:

I(x,y) = a(x,y)*f(x,y) + I(x-1,y) + I(x,y-1) - I(x-1,y-1).
Ia(x,y) = a(x,y) + Ia(x-1,y) + Ia(x,y-1) - Ia(x-1,y-1).

When x<0 or y<0, Ia(x,y)==0.

Rearrange, to get the action of "deintegim window 1x1":

a(x,y) = Ia(x,y) - Ia(x-1,y) - Ia(x,y-1) + Ia(x-1,y-1).

f(x,y) = (I(x,y) - I(x-1,y) - I(x,y-1) + I(x-1,y-1)) / a(x,y)

The more general case has larger windows:

winArea = (x₂-x₁)*(y₂-y₁)

k(x₁,y₁,x₂,y₂) = Ia(x₂,y₂) - Ia(x₂,y₁-1) - Ia(x₁-1,y₂) + Ia(x₁-1,y₁-1)

a(x₁,y₁,x₂,y₂) = k(x₁,y₁,x₂,y₂) / winArea

f(x₁,y₁,x₂,y₂) = (I(x₂,y₂) - I(x₂,y₁-1) - I(x₁-1,y₂) + I(x₁-1,y₁-1)) / k(x₁,y₁,x₂,y₂)

... with the exception that when k(...)==0, we set f(...) to black.

Hence, when an input to integim has an alpha, the result from deintegim will have the same alpha.

set WIND=window 101x101

%IM7DEV%magick ^
  %SRC_TR% ^
  -alpha on ^
  -process 'integim' ^
  -process 'deintegim %WIND%' ^
  +write ii_tt_di0.png ^
  -background gray(50%%) ^
  -layers flatten ^
  ii_tt_di0_g.png

%IM7DEV%magick ^
  %SRC_TR% ^
  -process 'integim premult no' ^
  -process 'deintegim postdiv no %WIND%' ^
  +write ii_tt_di1.png ^
  -background gray(50%%) ^
  -layers flatten ^
  ii_tt_di1_g.png

When we pre-multiply but don't post-divide, or don't pre-multiply but do post-divide, the results look okay against a white background but clearly not against a gray background: we see a dark or light halo in the semi-transparent areas.

%IM7DEV%magick ^
  %SRC_TR% ^
  -process 'integim premult yes' ^
  -process 'deintegim postdiv no %WIND%' ^
  +write ii_tt_di2.png ^
  -background gray(50%%) ^
  -layers flatten ^
  ii_tt_di2_g.png

%IM7DEV%magick ^
  %SRC_TR% ^
  -process 'integim premult no' ^
  -process 'deintegim postdiv yes %WIND%' ^
  +write ii_tt_di3.png ^
  -background gray(50%%) ^
  -layers flatten ^
  ii_tt_di3_g.png

We should be careful to use the same setting for both processes.

deintegim2

Precision

Non-integer window sizes

Displacement issue

Considering integim and deintegim as a single unit, each output pixel is the mean of a rectangle of the input pixels, where some pixel of the rectangle is in the same position as that output pixel.

Put another way, if the input has WxH pixels and the window is axb pixels, we could create (W+a-1)*(H*b-1) output pixels, and crop from there. The cumulhisto scripts work that way, because extending and cropping is the simplest method at the command level. But it is also expensive, when the real work needs only two passes over the image. So deintegim uses a rectangle centred on the given location, but crops the rectangle if needed so it doesn't extend beyond any image edge.

Scripts

For convenience, .bat scripts are also available in a single zip file. See Zipped BAT files.

integral.bat

This script is shown for interest. In practice, the integim process module is preferred.

rem From image %1, make integral %2.
rem Output should be capable of storing HDRI values.
rem %3 is optional window size, eg 5x7.
@rem
@rem Also uses:
@rem   iiREGARDALPHA if 1, uses alpha.
@rem
@rem See also deintegral.bat.
@rem
@rem Updated:
@rem   8-August-2022 for IM v7.
@rem



@if "%1"=="" findstr /B "rem @rem" %~f0 & exit /B 1

@setlocal enabledelayedexpansion

@call echoOffSave

call %PICTBAT%setInOut %1 integ

if not "%2"=="" if not "%2"=="." set OUTFILE=%2

call parseXxY2i 0 0 integ %3
if ERRORLEVEL 1 exit /B 1

if "%iiREGARDALPHA%"=="1" (
  set RA=regardalpha
) else (
  set RA=
)

set RA=

echo %0: integ_X=%integ_X% integ_Y=%integ_Y%

:: Setting the viewport adds the two fx: expressions as properties,
:: so this removes them.

%IM7DEV%magick ^
  %INFILE% ^
  -set colorspace sRGB ^
  -channel RGB ^
  -set option:distort:viewport ^
    "%%[fx:w+2*%integ_X%]x%%[fx:h+2*%integ_Y%]-%integ_X%-%integ_Y%" ^
  -virtual-pixel Edge ^
  -filter point ^
  +distort SRT 0 ^
  +repage ^
  -process 'cumulhisto %RA%' ^
  -rotate -90 ^
  -process 'cumulhisto %RA%' ^
  -rotate +90 ^
  +depth ^
  -define quantum:format=floating-point ^
+set fx:w+2*%integ_X% ^
+set fx:h+2*%integ_Y% ^
  +channel ^
  %OUTFILE%

if ERRORLEVEL 1 exit /B 1

call echoRestore

endlocal & set integOUTFILE=%OUTFILE%

deintegral.bat

This script is shown for interest. In practice, the integim process module is preferred.

rem From integral %1, make image %2.
rem Input should be capable of storing HDRI values.
rem %3 is optional window size, eg 5x7.
rem
rem See also integral.bat.
@rem
@rem Assumes magick is HDRI.
@rem
@rem Updated:
@rem   8-August-2022 for IM v7.
@rem


@if "%1"=="" findstr /B "rem @rem" %~f0 & exit /B 1

@setlocal enabledelayedexpansion

@call echoOffSave

call %PICTBAT%setInOut %1 deinteg

if not "%2"=="" if not "%2"=="." set OUTFILE=%2

call parseXxY2 0 0 deinteg %3

echo %0: deinteg_X=%deinteg_X% deinteg_Y=%deinteg_Y%

set crpW=
for /F "usebackq" %%L in (`%IMG7%magick identify ^
  -format "crpW=%%[fx:w-2*%deinteg_X%]\ncrpH=%%[fx:h-2*%deinteg_Y%]\n" ^
  %INFILE%`) do set %%L

if "%crpW%"=="" exit /B 1

set sCROP=-crop !crpW!x!crpH!+%deinteg_X%+%deinteg_Y% +repage

echo %0: sCROP=%sCROP%

%IMG7%magick ^
  %INFILE% ^
  ( -clone 0 -repage +1+0 ) ^
  ( -clone 0 -repage +0+1 ) ^
  ( -clone 0 -repage +1+1 ) ^
  -virtual-pixel Black ^
  -background None ^
  -define compose:clamp=off ^
  ( -clone 0-1 ^
    -compose MinusSrc -layers Flatten ^
    -clone 3 ^
    -compose Plus -layers Flatten ^
    -clone 2 ^
    -compose MinusSrc -layers Flatten ^
    +repage ^
  ) ^
  -delete 0-3 ^
  %sCROP% ^
  -alpha off ^
  -define quantum:format=floating-point ^
  %OUTFILE%

if ERRORLEVEL 1 exit /B 1

%IMG7%magick identify %OUTFILE%

call echoRestore

endlocal & set deintegOUTFILE=%OUTFILE%

integMean.bat

This script is shown for interest. In practice, the iiMeanSd.bat script is preferred.

rem From integral %1, make image %2, the windowed mean.
rem Input should be capable of storing HDRI values.
rem %3 is optional window size, eg 5x7.
@rem
@rem Also uses:
@rem   iiREGARDALPHA if 1, uses alpha.
@rem
@rem See also integral.bat.
@rem
@rem Updated:
@rem   8-August-2022 for IM v7.
@rem


@if "%1"=="" findstr /B "rem @rem" %~f0 & exit /B 1

@setlocal enabledelayedexpansion

@call echoOffSave

call %PICTBAT%setInOut %1 imn

if not "%2"=="" if not "%2"=="." set OUTFILE=%2

call parseXxY2i 0 0 imn %3
if ERRORLEVEL 1 exit /B 1

echo %0: imn_X=%imn_X% imn_Y=%imn_Y%

set /A dx1=(%imn_X%-1)/2
set /A dx0=%imn_X%-1-%dx1%

set /A dy1=(%imn_Y%-1)/2
set /A dy0=%imn_Y%-1-%dy1%

set /A WINAREA=%imn_X%*%imn_Y%

echo %0: %dx0% %dx1%  %dy0% %dy1% WINAREA=%WINAREA%

if "%iiREGARDALPHA%"=="1" (
  set sDIVIDE=^( +clone -alpha extract ^) -compose DivideSrc -composite
  set sDIVIDE=
) else (
  set sDIVIDE=-evaluate Divide %WINAREA%
)

set sDIVIDE=-set channel RGB -evaluate Divide %WINAREA% +channel

set /A xp1=%dx0%+1
set /A yp1=%dy0%+1

set crpW=
for /F "usebackq" %%L in (`%IMG7%magick identify ^
  -format "crpW=%%[fx:w-2*%imn_X%]\ncrpH=%%[fx:h-2*%imn_Y%]\n" ^
  %INFILE%`) do set %%L

if "%crpW%"=="" exit /B 1

set sCROP=-crop !crpW!x!crpH!+%imn_X%+%imn_Y% +repage

echo %0: sCROP=%sCROP%

%IMG7%magick ^
  %INFILE% ^
  ( -clone 0 -repage -%dx1%-%dy1% ) ^
  ( -clone 0 -repage -%dx1%+%yp1% ) ^
  ( -clone 0 -repage +%xp1%-%dy1% ) ^
  ( -clone 0 -repage +%xp1%+%yp1% ) ^
  -delete 0 ^
  -virtual-pixel Black ^
  -background None ^
  -define compose:clamp=off ^
  -alpha off ^
  ( -clone 0-1 ^
    -compose MinusSrc -layers Merge ^
    -clone 3 ^
    -compose Plus -layers Merge ^
    -clone 2 ^
    -compose MinusSrc -layers Merge ^
  ) ^
  -delete 0-3 ^
  %sCROP% ^
  %sDIVIDE% ^
  -alpha off ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  %OUTFILE%

if "%iiREGARDALPHA%"=="1" (
  %IMG7%magick ^
  %INFILE% ^
  -alpha extract ^
  ^( -clone 0 -repage -%dx1%-%dy1% ^) ^
  ^( -clone 0 -repage -%dx1%+%yp1% ^) ^
  ^( -clone 0 -repage +%xp1%-%dy1% ^) ^
  ^( -clone 0 -repage +%xp1%+%yp1% ^) ^
  -delete 0 ^
  -virtual-pixel Black ^
  -background None ^
  -define compose:clamp=off ^
  -alpha off ^
  ^( -clone 0-1 ^
    -compose MinusSrc -layers Merge ^
    -clone 3 ^
    -compose Plus -layers Merge ^
    -clone 2 ^
    -compose MinusSrc -layers Merge ^
  ^) ^
  -delete 0-3 ^
  %sCROP% ^
  %sDIVIDE% ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  %OUTFILE% ^
  -define compose:clamp=off ^
  -compose DivideDst -composite ^
  -define quantum:format=floating-point ^
  %OUTFILE%

)

if ERRORLEVEL 1 exit /B 1

call echoRestore

endlocal & set imnOUTFILE=%OUTFILE%

integMeanSd.bat

This script is shown for interest. In practice, the iiMeanSd.bat script is preferred.

rem From image %1
rem write windowed mean %2 and standard deviation %3
rem with window size %4
rem using the cumulhisto integral image method.
@rem
@rem Todo: reduce work if user doesn't want mean or SD.
@rem
@rem
@rem Updated:
@rem   8-August-2022 for IM v7.
@rem


@if "%4"=="" findstr /B "rem @rem" %~f0 & exit /B 1

@setlocal enabledelayedexpansion

@call echoOffSave

call %PICTBAT%setInOut %1 imnsd

set OUTMEAN=%2
if "%OUTMEAN%"=="." set OUTMEAN=
if "%OUTMEAN%"=="" set OUTMEAN=

set OUTSD=%3
if "%OUTSD%"=="." set OUTSD=
if "%OUTSD%"=="" set OUTSD=

set WINDIMS=%4

:: Temporary mean of square, and square of mean.
set TMPDIR=\temp\
set TMP_MN_SQ=%TMPDIR%ims_ms.miff
set TMP_MN_SQ2=%TMPDIR%ims_ms2.miff
set TMP_MN_SQ3=%TMPDIR%ims_ms3.miff
set TMP_SQ_MN=%TMPDIR%ims_sm.miff

if "%OUTMEAN%"=="" (
  set wrOUTMEAN=
) else (
  set wrOUTMEAN=+write %OUTMEAN%
)

%IMG7%magick ^
  %INFILE% ^
  -evaluate Pow 2 ^
  +depth ^
  -depth 32 ^
  -define quantum:format=floating-point ^
  %TMP_MN_SQ%

if ERRORLEVEL 1 exit /B 1

call %PICTBAT%integral %TMP_MN_SQ% %TMP_MN_SQ2% %WINDIMS%
if ERRORLEVEL 1 exit /B 1

call %PICTBAT%integMean %TMP_MN_SQ2% %TMP_MN_SQ3% %WINDIMS%
if ERRORLEVEL 1 exit /B 1


call %PICTBAT%integral %INFILE% %TMP_SQ_MN% %WINDIMS%
if ERRORLEVEL 1 exit /B 1

call %PICTBAT%integMean %TMP_SQ_MN% %TMP_SQ_MN% %WINDIMS%
if ERRORLEVEL 1 exit /B 1

if ERRORLEVEL 1 exit /B 1

if "%OUTSD%"=="" (
  set sSQFORSD=NULL:
) else (
  set sSQFORSD=-evaluate Pow 2 %TMP_SQ_MN%
)


%IMG7%magick ^
  %TMP_SQ_MN% ^
  %wrOUTMEAN% ^
  %sSQFORSD%

if ERRORLEVEL 1 exit /B 1

if not "%OUTSD%"=="" %IMG7%magick ^
  %TMP_MN_SQ3% ^
  %TMP_SQ_MN% ^
  -compose MinusSrc -composite ^
  -evaluate Pow 0.5 ^
  %OUTSD%


call echoRestore

endlocal

iiMeanSd.bat

rem From image %1
rem write windowed mean %2
rem and standard deviation %3
rem with window size %4 eg 20x20
rem using the process module integral image method.
@rem
@rem Updated:
@rem   8-August-2022 for IM v7.
@rem


@if "%4"=="" findstr /B "rem @rem" %~f0 & exit /B 1

@setlocal enabledelayedexpansion

rem @call echoOffSave

call %PICTBAT%setInOut %1 rmnsd

set OUTMEAN=%2
if "%OUTMEAN%"=="." set OUTMEAN=
if "%OUTMEAN%"=="" set OUTMEAN=

set OUTSD=%3
if "%OUTSD%"=="." set OUTSD=
if "%OUTSD%"=="" set OUTSD=

set WINDIMS=%4

if "%OUTMEAN%"=="" (
  set wrOUTMEAN=
) else (
  set wrOUTMEAN=+write %OUTMEAN%
)

if "%OUTSD%"=="" (

  %IM7DEV%magick ^
    %INFILE% ^
    -process 'integim' ^
    -process 'deintegim window %WINDIMS%' ^
    -depth 32 ^
    -define quantum:format=floating-point ^
    %wrOUTMEAN% ^
    NULL:

) else (

  %IM7DEV%magick ^
    %INFILE% ^
    -depth 32 ^
    -define quantum:format=floating-point ^
    ^( -clone 0 ^
       -evaluate Pow 2 ^
       -process 'integim' ^
       -process 'deintegim window %WINDIMS%' ^
    ^) ^
    ^( -clone 0 ^
       -process 'integim' ^
       -process 'deintegim window %WINDIMS%' ^
       %wrOUTMEAN% ^
       -evaluate Pow 2 ^
    ^) ^
    -delete 0 ^
    -alpha off ^
    -compose MinusSrc -composite ^
    -evaluate Pow 0.5 ^
    %OUTSD%
)

call echoRestore

endlocal

parseXxY2.bat

rem Parses %4, default %1 and %2. Returns %3_X and %3_Y.
@rem
@rem %1 and %2 can be expressions such as "600-1".
@rem
@rem %4 is one of these formats:
@rem   {blank}
@rem   .
@rem   {number}
@rem   {number}x
@rem   x{number}
@rem   {number}x{number}
@rem
@rem Each number can be suffixed with %, c or p or C or P.
@rem
@rem Updated:
@rem   4-October-2022 for IM v7.
@rem   20-August-2023 Put %1 and %2 in parentheses so they can be expressions.
@rem

@set pxxy=%4
@set pxxyFirst=%pxxy:~0,1%
@rem echo pxxyFirst=%pxxyFirst%

@if "%pxxyFirst%"=="x" set pxxy=%1%pxxy%

@if "%pxxy%"=="." set pxxy=
@if "%pxxy%"=="" set pxxy=%1x%2

@for /F "usebackq tokens=1-2 delims=xX" %%X in ('%pxxy%') do @(
  @rem echo %%X,%%Y
  @set pxxyX=%%X
  @set pxxyY=%%Y
)
@if "%pxxyY%"=="" set pxxyY=%2


set CH_LAST=%pxxyX:~-1%

if "%CH_LAST%"=="^%" set CH_LAST=c

if /I "%CH_LAST%"=="c" (
  for /F "usebackq" %%L in (`%IMG7%magick identify ^
    -precision 19 ^
    -format "pxxyX=%%[fx:(%1)*%pxxyX:~0,-1%/100]" ^
    xc:`) do set %%L

) else if /I "%CH_LAST%"=="p" (
  for /F "usebackq" %%L in (`%IMG7%magick identify ^
    -precision 19 ^
    -format "pxxyX=%%[fx:(%1)*%pxxyX:~0,-1%]" ^
    xc:`) do set %%L
)


set CH_LAST=%pxxyY:~-1%

if "%CH_LAST%"=="^%" set CH_LAST=c

if /I "%CH_LAST%"=="c" (
  for /F "usebackq" %%L in (`%IMG7%magick identify ^
    -precision 19 ^
    -format "pxxyY=%%[fx:(%2)*%pxxyY:~0,-1%/100]" ^
    xc:`) do set %%L

) else if /I "%CH_LAST%"=="p" (
  for /F "usebackq" %%L in (`%IMG7%magick identify ^
    -precision 19 ^
    -format "pxxyY=%%[fx:(%2)*%pxxyY:~0,-1%]" ^
    xc:`) do set %%L
)


@rem echo pxxyX=%pxxyX% pxxyY=%pxxyY%

set %3_X=%pxxyX%
set %3_Y=%pxxyY%

parseXxY2i.bat

rem Like parseXxY2.bat, but rounds numbers to integers.
@rem
@rem Updated:
@rem   4-October-2022 for IM v7.
@rem

call parseXxY2 %1 %2 %3 %4

for /F "usebackq" %%L in (`%IMG7%magick identify ^
  -precision 19 ^
  -format "%3_X=%%[fx:int(!%3_X!+0.5)]\n%3_Y=%%[fx:int(!%3_Y!+0.5)]\n" ^
  xc:`) do set %%L

if ERRORLEVEL 1 exit /B 1

deOutlier.bat

rem From image %1,
rem make %2
rem replacing pixels outside range (mean plus or minus k*SD) by range limit.
rem %3 window dimensions, WxH 
rem %4 k, typically 1.0 to 3.0 [default 2].
rem %5 post-processing, eg "-auto-level".
@rem
@rem Updated:
@rem   8-August-2022 for IM v7.
@rem

@if "%1"=="" findstr /B "rem @rem" %~f0 & exit /B 1

@setlocal enabledelayedexpansion

@call echoOffSave

call %PICTBAT%setInOut %1 do

if not "%2"=="" if not "%2"=="." set OUTFILE=%2

set WINDIMS=%3
if "%WINDIMS%"=="." set WINDIMS=
if "%WINDIMS%"=="" set WINDIMS=10x10

set K=%4
if "%K%"=="." set K=
if "%K%"=="" set K=2

set POSTPROC=%~5
if "%POSTPROC%"=="." set POSTPROC=

%IM7DEV%magick ^
  %INFILE% ^
  +write mpr:SRC ^
  +delete ^
  ( mpr:SRC ^
    -depth 32 ^
    -define quantum:format=floating-point ^
    ^( -clone 0 ^
       -evaluate Pow 2 ^
       -process 'integim' ^
       -process 'deintegim window %WINDIMS%' ^
    ^) ^
    ^( -clone 0 ^
       -process 'integim' ^
       -process 'deintegim window %WINDIMS%' ^
       +write mpr:MEAN ^
       -evaluate Pow 2 ^
    ^) ^
    -delete 0 ^
    -alpha off ^
    -compose MinusSrc -composite ^
    -evaluate Pow 0.5 ^
    +write mpr:SD ^
    +delete ^
  ) ^
  mpr:MEAN ^
  mpr:SD ^
  ( -clone 0-1 ^
    -compose Mathematics ^
    -define compose:args=0,-%K%,1,0 -composite ^
    mpr:SRC ^
    -evaluate-sequence Max ^
  ) ^
  ( -clone 0-1 ^
    -compose Mathematics ^
    -define compose:args=0,%K%,1,0 -composite ^
  ) ^
  -delete 0-1 ^
  -evaluate-sequence Min ^
  %POSTPROC% ^
  %OUTFILE%

if ERRORLEVEL 1 exit /B 1

call echoRestore

endlocal & set doOUTFILE=%OUTFILE%

All images on this page were created by the commands shown, using:

%IMG7%magick -version

Version: ImageMagick 7.1.1-20 Q16-HDRI x86 98bb1d4:20231008 https://imagemagick.org
Copyright: (C) 1999 ImageMagick Studio LLC
License: https://imagemagick.org/script/license.php
Features: Cipher DPC HDRI OpenCL OpenMP(2.0) 
Delegates (built-in): bzlib cairo freetype gslib heic jng jp2 jpeg jxl lcms lqr lzma openexr pangocairo png ps raqm raw rsvg tiff webp xml zip zlib
Compiler: Visual Studio 2022 (193532217)

%IM7DEV%magick -version

Version: ImageMagick 7.1.0-33 beta Q32-HDRI x86_64 64b5fe68a:20220501 https://imagemagick.org
Copyright: (C) 1999 ImageMagick Studio LLC
License: https://imagemagick.org/script/license.php
Features: Cipher DPC HDRI Modules OpenMP(4.5) 
Delegates (built-in): bzlib fpx jbig jpeg lcms ltdl lzma tiff webp x xml zip zlib
Compiler: gcc (11.3)

To improve internet download speeds, some images may have been automatically converted (by ImageMagick, of course) from PNG or TIFF or MIFF to JPG.

Source file for this web page is integim.h1. To re-create this web page, execute "procH1 integim".

This page, including the images except where shown otherwise, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.

Anyone is permitted to re-publish this page, but only for non-commercial use.

Anyone is permitted to link to this page, including for commercial use.

Page version v2.0 22-July-2017.

Page created 01-Mar-2024 15:12:43.