snibgo's ImageMagick pages
Log cluts
Applying log transformations to cluts.
This page logically follows from
Clut cookbook. Here, we consider only cluts that are something like y=logb(x), and their inverses that are something like x=by.
See also
Non-absolute cluts.
When the domain of x is [0,1], log(x) ranges from minus infinity to 0, [-∞,0]. We can't easily transform from [-∞,0] to [0,1]. To avoid the problem with infinity, we introduce a small number ε (epsilon) into the equations, making curves that have different trade-offs.
This page show three methods for using epsilon:
add,
spread or
skip.
We add a small value ε (epsilon) to x before taking the log, so the range would be log(ε) to log(1+ε). A subtraction and division normalises the output to [0,1].
y = log(x+ε)-log(ε)
log(1+ε)-log(ε)
= log((x+ε)/ε)
log((1+ε)/ε)
For the reverse:
log(x+ε) = y * log((1+ε)/ε) + log(ε)
= log((1+ε)^y/ε^y) + log(ε)
= log((1+ε)^y/ε^(y-1))
x+ε = (1+ε)^y
ε^(y-1)
x = (1+ε)^y - ε
ε^(y-1)
... where b is the base of the logarithms. Any base can be used; the result is the same.
|
Forwards:
set WW=256
set Eps=(1/%WW%)
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "LE=logtwo(%Eps%);(logtwo(u+%Eps%)-LE)/(logtwo(1+%Eps%)-LE)" ^
lgcl_log1.png
call %PICTBAT%graph1d lgcl_log1.png
|

|
|
Reverse:
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "pow(1+%Eps%,u)/pow(%Eps%,u-1)-%Eps%" ^
lgcl_log2.png
call %PICTBAT%graph1d lgcl_log2.png
|

|
We test the round-trip:
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
( +clone ^
-fx "LE=logtwo(%Eps%);(logtwo(u+%Eps%)-LE)/(logtwo(1+%Eps%)-LE)" ^
-fx "pow(1+%Eps%,u)/pow(%Eps%,u-1)-%Eps%" ^
) ^
-metric RMSE ^
-format %%[distortion] ^
-compare ^
info:
5.78401e-08
The round-trip is accurate.
Test intervals:
set WW=4096
set Eps=(1/%WW%)
set Eps=(1e-14)
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "LE=logtwo(%Eps%);(logtwo(u+%Eps%)-LE)/(logtwo(1+%Eps%)-LE)" ^
( -clone 0 -crop 1x1+4095+0 ) ^
( -clone 0 -crop 1x1+2048+0 ) ^
( -clone 0 -crop 1x1+1024+0 ) ^
( -clone 0 -crop 1x1+512+0 ) ^
( -clone 0 -crop 1x1+256+0 ) ^
( -clone 0 -crop 1x1+128+0 ) ^
( -clone 0 -crop 1x1+64+0 ) ^
( -clone 0 -crop 1x1+32+0 ) ^
( -clone 0 -crop 1x1+16+0 ) ^
( -clone 0 -crop 1x1+8+0 ) ^
( -clone 0 -crop 1x1+4+0 ) ^
( -clone 0 -crop 1x1+2+0 ) ^
( -clone 0 -crop 1x1+1+0 ) ^
-delete 0 ^
+append +repage ^
txt:
# ImageMagick pixel enumeration: 13,1,0,65535,srgb
0,0: (65535,65535,65535) #FFFFFFFFFFFF white
1,0: (64126,64126,64126) #FA7EFA7EFA7E srgb(97.8505%,97.8505%,97.8505%)
2,0: (62717,62717,62717) #F4FDF4FDF4FD srgb(95.7003%,95.7003%,95.7003%)
3,0: (61308,61308,61308) #EF7CEF7CEF7C srgb(93.5501%,93.5501%,93.5501%)
4,0: (59899,59899,59899) #E9FBE9FBE9FB srgb(91.3999%,91.3999%,91.3999%)
5,0: (58490,58490,58490) #E47AE47AE47A srgb(89.2497%,89.2497%,89.2497%)
6,0: (57081,57081,57081) #DEF9DEF9DEF9 srgb(87.0995%,87.0995%,87.0995%)
7,0: (55671,55671,55671) #D977D977D977 srgb(84.9493%,84.9493%,84.9493%)
8,0: (54262,54262,54262) #D3F6D3F6D3F6 srgb(82.799%,82.799%,82.799%)
9,0: (52853,52853,52853) #CE75CE75CE75 srgb(80.6488%,80.6488%,80.6488%)
10,0: (51444,51444,51444) #C8F4C8F4C8F4 srgb(78.4986%,78.4986%,78.4986%)
11,0: (50035,50035,50035) #C373C373C373 srgb(76.3484%,76.3484%,76.3484%)
12,0: (48626,48626,48626) #BDF2BDF2BDF2 srgb(74.1982%,74.1982%,74.1982%)
An alternative method first transforms the input from [0,1] to [ε,1], so the range would be [log(ε),0]. We divide by -log(ε) to make the range [-1,0], then add 1.0 so the range is [0,1].
UU = x + (1-x) * ε
= x + ε - x * ε
= x * (1 - ε) + ε
y = log(UU) + 1
-log(ε)
For the reverse:
log(UU) = (1-y)*log(ε)
UU = pow(b, (1-y)*log(ε))
= pow(b, log(ε^(1-y)))
= ε^(1-y)
x = UU - ε
1 - ε
= pow(b, (1-y)*log(ε)) - ε
1 - ε
= ε^(1-y) - ε
1 - ε
... where b is the base of the logarithms. Any base can be used; the result is the same.
|
Forwards:
set WW=256
set Eps=(1/%WW%)
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "UU=u+(1-u)*%Eps%;-log(UU)/log(%Eps%)+1" ^
lgcl_logdif1.png
call %PICTBAT%graph1d lgcl_logdif1.png
|

|
|
Reverse:
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "(pow(%Eps%,1-u)-%Eps%)/(1-%Eps%)" ^
lgcl_logdif2.png
call %PICTBAT%graph1d lgcl_logdif2.png
|

|
We test the round-trip:
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
( +clone ^
-fx "UU=u+(1-u)*%Eps%;-log(UU)/log(%Eps%)+1" ^
-fx "(pow(%Eps%,1-u)-%Eps%)/(1-%Eps%)" ^
) ^
-metric RMSE ^
-format %%[distortion] ^
-compare ^
info:
5.80932e-08
The round-trip is accurate.
Test intervals:
set WW=4096
set Eps=(1/%WW%)
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "UU=u+(1-u)*%Eps%;-log(UU)/log(%Eps%)+1" ^
( -clone 0 -crop 1x1+4095+0 ) ^
( -clone 0 -crop 1x1+2048+0 ) ^
( -clone 0 -crop 1x1+1024+0 ) ^
( -clone 0 -crop 1x1+512+0 ) ^
( -clone 0 -crop 1x1+256+0 ) ^
( -clone 0 -crop 1x1+128+0 ) ^
( -clone 0 -crop 1x1+64+0 ) ^
( -clone 0 -crop 1x1+32+0 ) ^
( -clone 0 -crop 1x1+16+0 ) ^
( -clone 0 -crop 1x1+8+0 ) ^
( -clone 0 -crop 1x1+4+0 ) ^
( -clone 0 -crop 1x1+2+0 ) ^
( -clone 0 -crop 1x1+1+0 ) ^
-delete 0 ^
+append +repage ^
txt:
# ImageMagick pixel enumeration: 13,1,0,65535,srgb
0,0: (65535,65535,65535) #FFFFFFFFFFFF white
1,0: (60078,60078,60078) #EAAEEAAEEAAE srgb(91.6725%,91.6725%,91.6725%)
2,0: (54620,54620,54620) #D55CD55CD55C srgb(83.3451%,83.3451%,83.3451%)
3,0: (49167,49167,49167) #C00FC00FC00F srgb(75.0235%,75.0235%,75.0235%)
4,0: (43721,43721,43721) #AAC9AAC9AAC9 srgb(66.7135%,66.7135%,66.7135%)
5,0: (38290,38290,38290) #959295929592 srgb(58.4269%,58.4269%,58.4269%)
6,0: (32890,32890,32890) #807A807A807A srgb(50.1864%,50.1864%,50.1864%)
7,0: (27549,27549,27549) #6B9D6B9D6B9D srgb(42.0366%,42.0366%,42.0366%)
8,0: (22323,22323,22323) #573357335733 srgb(34.0622%,34.0622%,34.0622%)
9,0: (17312,17312,17312) #43A043A043A0 srgb(26.416%,26.416%,26.416%)
10,0: (12681,12681,12681) #318931893189 srgb(19.3494%,19.3494%,19.3494%)
11,0: (8656,8656,8656) #21D021D021D0 srgb(13.208%,13.208%,13.208%)
12,0: (5461,5461,5461) #155515551555 srgb(8.33333%,8.33333%,8.33333%)
A third method passes through (ε,0) and (1,1). At x<ε, y is negative. This is a true log curve, with the property that a given multiplication to x will result in a constant addition to y. However, the curve passes through (0,-∞) instead of (0,0).
Forwards:
y = log(x/ε)
log(1/ε)
Reverse:
x = ε * pow(b,log(1/ε)*y)
= ε * (1/ε)^y
= 1 / ε^(y-1)
= ε^(1-y)
... where b is the base of the logarithms. Any base can be used; the result is the same.
|
Forwards:
set WW=256
set Eps=(1/%WW%)
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "log(u/%Eps%)/log(1/%Eps%)" ^
lgcl_logdif3.png
call %PICTBAT%graph1d lgcl_logdif3.png
|

|
|
Reverse:
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "pow(%Eps%,(1-u))" ^
lgcl_logdif4.png
call %PICTBAT%graph1d lgcl_logdif4.png
|

|
We test the round-trip, with the reverse transformation first:
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
( +clone ^
-fx "pow(%Eps%,(1-u))" ^
-fx "log(u/%Eps%)/log(1/%Eps%)" ^
) ^
-metric RMSE ^
-format %%[distortion] ^
-compare ^
info:
2.27554e-09
The round-trip is accurate.
Test intervals in the forwards direction:
set WW=4096
set Eps=(1/%WW%)
%IMG7%magick ^
-size %WW%x1 gradient:black-white ^
-fx "log(u/%Eps%)/log(1/%Eps%)" ^
( -clone 0 -crop 1x1+4095+0 ) ^
( -clone 0 -crop 1x1+2048+0 ) ^
( -clone 0 -crop 1x1+1024+0 ) ^
( -clone 0 -crop 1x1+512+0 ) ^
( -clone 0 -crop 1x1+256+0 ) ^
( -clone 0 -crop 1x1+128+0 ) ^
( -clone 0 -crop 1x1+64+0 ) ^
( -clone 0 -crop 1x1+32+0 ) ^
( -clone 0 -crop 1x1+16+0 ) ^
( -clone 0 -crop 1x1+8+0 ) ^
( -clone 0 -crop 1x1+4+0 ) ^
( -clone 0 -crop 1x1+2+0 ) ^
( -clone 0 -crop 1x1+1+0 ) ^
-delete 0 ^
+append +repage ^
txt:
# ImageMagick pixel enumeration: 13,1,0,65535,srgb
0,0: (65535,65535,65535) #FFFFFFFFFFFF white
1,0: (60076,60076,60076) #EAACEAACEAAC srgb(91.6696%,91.6696%,91.6696%)
2,0: (54614,54614,54614) #D556D556D556 srgb(83.3363%,83.3363%,83.3363%)
3,0: (49153,49153,49153) #C001C001C001 srgb(75.0029%,75.0029%,75.0029%)
4,0: (43692,43692,43692) #AAACAAACAAAC srgb(66.6696%,66.6696%,66.6696%)
5,0: (38231,38231,38231) #955795579557 srgb(58.3363%,58.3363%,58.3363%)
6,0: (32769,32769,32769) #800180018001 srgb(50.0029%,50.0029%,50.0029%)
7,0: (27308,27308,27308) #6AAC6AAC6AAC srgb(41.6696%,41.6696%,41.6696%)
8,0: (21847,21847,21847) #555755575557 srgb(33.3363%,33.3363%,33.3363%)
9,0: (16386,16386,16386) #400240024002 srgb(25.0029%,25.0029%,25.0029%)
10,0: (10924,10924,10924) #2AAC2AAC2AAC srgb(16.6696%,16.6696%,16.6696%)
11,0: (5463,5463,5463) #155715571557 srgb(8.33627%,8.33627%,8.33627%)
12,0: (2,2,2) #000200020002 srgb(0.00293486%,0.00293486%,0.00293486%)
As noted above, a given multiplication to x will result in a constant addition to y. In the forwards direction, if x2 = k * x1, what is y2-y1?
y2-y1 = log(x1*k/ε) - log(x1/ε)
log(1/ε) log(1/ε)
= log(x1*k/ε) - log(x1/ε)
log(1/ε)
= log(k)
log(1/ε)
For example, x doubles (k=2) at y intervals of log(2)/log(1/(1/4096)) = 0.08333 (as a fraction of the height, on a scale of 0 to 1).
If we want to add tick-marks or grid lines at every doubling, how many marks do we need? We need floor(logk(1/ε)+0.5) marks, where k=2 for doubling.
The reverse and forwards log transformations can be used to alter the input or output of any clut. When expressed as a graph, this shifts what was at 50% of the input towards the right, or 50% of the output towards the top. We can use any of the above methods:
Add epsilon,
Spread epsilon or
Skip epsilon.
Note that we use the reverse log transformation on the input, and the forwards log transformation on the output.
For example, using the
Add epsilon method to modify an S-shape curve:
|
No log transformation:
set mscPREPROC=
set mscPOSTPROC=
call %PICTBAT%mSigClut lgcl_lognone.png 256 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_lognone.png
|

|
|
log(x) pushes the curve to the right:
set WW=256
set Eps=(1/%WW%)
set mscPREPROC=-fx "pow(1+%Eps%,u)/pow(%Eps%,u-1)-%Eps%"
set mscPOSTPROC=
call %PICTBAT%mSigClut lgcl_logx.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logx.png
|

|
|
log(y) pushes the curve to the top:
set mscPREPROC=
set mscPOSTPROC=-fx "LE=logtwo(%Eps%);(logtwo(u+%Eps%)-LE)/(logtwo(1+%Eps%)-LE)"
call %PICTBAT%mSigClut lgcl_logy.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logy.png
|

|
|
log(x) and log(y) pushes the curve to the top and right:
set mscPREPROC=-fx "pow(1+%Eps%,u)/pow(%Eps%,u-1)-%Eps%"
set mscPOSTPROC=-fx "LE=logtwo(%Eps%);(logtwo(u+%Eps%)-LE)/(logtwo(1+%Eps%)-LE)"
call %PICTBAT%mSigClut lgcl_logxy.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logxy.png
|

|
The
Add epsilon curve passes through (0,0) and (1,1) but does not have the property that a distance along the axis represents the same factor, for any place on the axis.
The
Skip epsilon method does have that property, but does not pass through (0,0).
|
log(x) pushes the curve to the right:
set WW=256
set Eps=(1/64)
set mscPREPROC=-fx "pow(%Eps%,(1-u))"
set mscPOSTPROC=
call %PICTBAT%mSigClut lgcl_logx2.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logx2.png
|

|
|
log(y) pushes the curve to the top:
set mscPREPROC=
set mscPOSTPROC=-fx "log(u/%Eps%)/log(1/%Eps%)"
call %PICTBAT%mSigClut lgcl_logy2.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logy2.png
|

|
|
log(x) and log(y) pushes the curve to the top and right:
set mscPREPROC=-fx "pow(%Eps%,(1-u))"
set mscPOSTPROC=-fx "log(u/%Eps%)/log(1/%Eps%)"
call %PICTBAT%mSigClut lgcl_logxy2.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logxy2.png
|

|
We can annotate the graphs with grid lines and axis labels. Each halving is shown with a grid line. The maximum value is labelled "0", as it represents 20 = 1. The next grid line would be labelled "-1" as it represents 2-1 = 0.5, the next "-2" as it represents 2-2 = 0.25, and so on.
|
log(x) pushes the curve to the right:
set WW=256
set Eps=(1/64)
set mscPREPROC=-fx "pow(%Eps%,(1-u))"
set mscPOSTPROC=
call %PICTBAT%mSigClut lgcl_logx3.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logx3.png . . . none
call %PICTBAT%gridHigh ^
lgcl_logx3_g1d.png lgcl_logx3_g1d.png x w/logtwo(1/%Eps%)
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-precision 2 ^
-format "LabLeft=%%[fx:-logtwo(1/%Eps%)]" ^
xc:`) do set %%L
call %PICTBAT%graph4labels ^
lgcl_logx3_g1d.png lgcl_logx3_g1d.png %LabLeft% 0
|
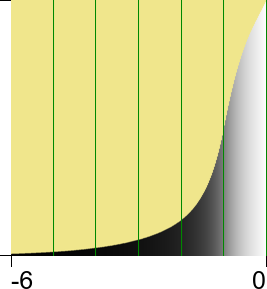
|
|
log(y) pushes the curve to the top:
set mscPREPROC=
set mscPOSTPROC=-fx "log(u/%Eps%)/log(1/%Eps%)"
call %PICTBAT%mSigClut lgcl_logy3.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logy3.png . . . none
call %PICTBAT%gridHigh ^
lgcl_logy3_g1d.png lgcl_logy3_g1d.png y h/logtwo(1/%Eps%)
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-precision 2 ^
-format "LabBottom=%%[fx:-logtwo(1/%Eps%)]" ^
xc:`) do set %%L
call %PICTBAT%graph4labels ^
lgcl_logy3_g1d.png lgcl_logy3_g1d.png . . %LabBottom% 0
|
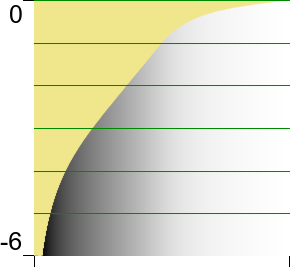
|
|
log(x) and log(y) pushes the curve to the top and right:
set mscPREPROC=-fx "pow(%Eps%,(1-u))"
set mscPOSTPROC=-fx "log(u/%Eps%)/log(1/%Eps%)"
call %PICTBAT%mSigClut lgcl_logxy3.png %WW% 0.5 0.5 0.5 4
call %PICTBAT%graph1d lgcl_logxy3.png . . . none
call %PICTBAT%gridHigh ^
lgcl_logxy3_g1d.png lgcl_logxy3_g1d.png both w/logtwo(1/%Eps%)
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-precision 2 ^
-format "LabLeft=%%[fx:-logtwo(1/%Eps%)]\nLabBottom=%%[fx:-logtwo(1/%Eps%)]\n" ^
xc:`) do set %%L
call %PICTBAT%graph4labels ^
lgcl_logxy3_g1d.png lgcl_logxy3_g1d.png %LabLeft% 0 %LabBottom% 0
|
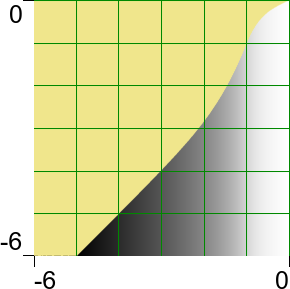
|
For convenience, .bat scripts are also available in a single zip file. See
Zipped BAT files.
rem Draws grid starting from top and/or right at given interval.
rem
rem %1 Input graph image
rem %2 Output image
rem %3 x or y or both
rem %4 interval in pixels between grid lines (can be expression for fx)
rem %5 colour for grid lines
@if "%1"=="" findstr /B "rem @rem" %~f0 & exit /B 1
@setlocal enabledelayedexpansion
@call echoOffSave
call %PICTBAT%setInOut %1 gdhi
if not "%2"=="" if not "%2"=="." set OUTFILE=%1
set WHICH=%3
if "%WHICH%"=="." set WHICH=
if "%WHICH%"=="" set WHICH=both
set INTVL=%4
if "%INTVL%"=="." set INTVL=
if "%INTVL%"=="" set INTVL=10
set COL=%5
if "%COL%"=="" set COL=
if "%COL%"=="" set COL=#0f08
echo %0: %WHICH% %INTVL% %COL%
set doX=0
set doY=0
if /I %WHICH%==x (
set doX=1
) else if /I %WHICH%==y (
set doY=1
) else if /I %WHICH%==both (
set doX=1
set doY=1
) else (
echo %0: error in WHICH [%WHICH%]
exit /B 1
)
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-precision 15 ^
-format "pxINTVL=%%[fx:%INTVL%]\nWW=%%w\nHH=%%h\nWm1=%%[fx:w-1]\nHm1=%%[fx:h-1]\n" ^
%INFILE%`) do set %%L
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-format "numX=%%[fx:floor(%WW%/%pxINTVL%)]\nnumY=%%[fx:floor(%HH%/%pxINTVL%)]\n" ^
xc:`) do set %%L
echo %0: WW=%WW% HH=%HH% pxINTVL=%pxINTVL% numX=%numX% numY=%numY%
set sLINES=
if %doX%==1 (
echo %0: doing X
set px=%Wm1%
set pxi=%Wm1%
for /L %%N in (0,1,%numX%) do (
set FIRSTCH=!pxi:~0,5!
if not !FIRSTCH!==- set sLINES=!sLINES! line !pxi!,0,!pxi!,%Hm1%
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-precision 15 ^
-format "px=%%[fx:!px!-%pxINTVL%]\npxi=%%[fx:floor(!px!-%pxINTVL%+0.5)]\n" ^
xc:`) do set %%L
)
)
if %doY%==1 (
echo %0: doing Y
set px=%Hm1%
set pxi=%Hm1%
set pxn=0
for /L %%N in (0,1,%numY%) do (
set FIRSTCH=!pxi:~0,5!
if not !FIRSTCH!==- set sLINES=!sLINES! line 0,!pxn!,%Wm1%,!pxn!
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-format "px=%%[fx:!px!-%pxINTVL%]\npxi=%%[fx:floor(!px!-%pxINTVL%+0.5)]\n" ^
xc:`) do set %%L
for /F "usebackq" %%L in (`%IMG7%magick identify ^
-format "pxn=%%[fx:%Hm1%-!pxi!]\n" ^
xc:`) do set %%L
)
)
echo %1: %sLINES%
%IMG7%magick ^
%INFILE% ^
-stroke %COL% ^
-draw "%sLINES%" ^
%OUTFILE%
call echoRestore
@endlocal
rem %1 output filename
rem %2 output width, pixels [4096]
rem %3 a, an input fraction [0.5]
rem %4 b, an output fraction [0.5]
rem %5 s, slope at both ends
rem %6 E, contrast strength, > 0
@rem 1 for straight line,
@rem >1 increases contrast at mid point
@rem <1 decreases contrast at mid point
@rem Values v and 1/v are symmetrical.
@rem
@rem Inflection is at (a,b).
@rem
@rem Also uses:
@rem mscPREPROC IM process applied to input linear grayscale
@rem mscPOSTPROC IM process applied to output
@rem
@rem Updated:
@rem 24-August-2022 for IM v7.
@rem
@if "%1"=="" findstr /B "rem @rem" %~f0 & exit /B 1
@setlocal enabledelayedexpansion
@call echoOffSave
call %PICTBAT%setInOut %1 msc
if not "%1"=="" if not "%1"=="." set OUTFILE=%1
set WW=%2
if "%WW%"=="." set WW=
if "%WW%"=="" set WW=4096
set a=%3
if "%a%"=="." set a=
if "%a%"=="" set a=0.5
set b=%4
if "%b%"=="." set b=
if "%b%"=="" set b=0.5
set s=%5
if "%s%"=="." set s=
if "%s%"=="" set s=1
set E=%6
if "%E%"=="." set E=
if "%E%"=="" set E=3
set a1=(1-%a%)
set s1=(1-%s%)
set sa=%s%*%a%
set sa1=%s%*%a1%
set LR=log(%b%)/log(%a%)
set LR1=log(1-%b%)/log(1-%a%)
for /F "usebackq" %%L in (`%IMG7%magick identify
-precision 15 ^
-format "a1=%%[fx:%a1%]\ns1=%%[fx:%s1%]\nsa=%%[fx:%sa%]\nsa1=%%[fx:%sa1%]" ^
xc:`) do set %%L
for /F "usebackq" %%L in (`%IMG7%magick identify
-precision 15 ^
-format "LR=%%[fx:%LR%]\nLR1=%%[fx:%LR1%]" ^
xc:`) do set %%L
%IMG7%magick -size 1x%WW% gradient: -rotate 90 ^
%mscPREPROC% ^
-fx "u<%a%?pow(%s1%*u+%sa%*pow(u/%a%,%E%),%LR%):1-pow(%s1%*(1-u)+%sa1%*pow((1-u)/%a1%,%E%),%LR1%)" ^
%mscPOSTPROC% ^
%OUTFILE%
rem call %PICTBAT%graph1d %OUTFILE%
call echoRestore
@endlocal
rem %1 input graph
rem %2 output
rem %3 min x label
rem %4 max x label
rem %5 min y label
rem %6 max y label
set INFILE=%1
set OUTFILE=%2
if "%OUTFILE%"=="." set OUTFILE=
set MINX=%~3
set MAXX=%~4
set MINY=%~5
set MAXY=%~6
if [%MINX%]==[.] set MINX=
if [%MAXX%]==[.] set MAXX=
if [%MINY%]==[.] set MINY=
if [%MAXY%]==[.] set MAXY=
if "%g4lPNTSZ%"=="." set g4lPNTSZ=
if "%g4lPNTSZ%"=="" set g4lPNTSZ=25
if "%g4lLINELEN%"=="." set g4lLINELEN=
if "%g4lLINELEN%"=="" set g4lLINELEN=10
if "%g4lBACKCOL%"=="." set g4lBACKCOL=
if "%g4lBACKCOL%"=="" set g4lBACKCOL=None
if "%MINX%"=="" (
set sMINX=
) else (
set sMINX=-gravity NorthWest -annotate +0+%g4lLINELEN% "%MINX%"
)
if "%MAXX%"=="" (
set sMAXX=
) else (
set sMAXX=-gravity NorthEast -annotate +0+%g4lLINELEN% "%MAXX%"
)
if "%MINY%"=="" (
set sMINY=
) else (
set sMINY=-gravity SouthEast -annotate +%g4lLINELEN%+0 "%MINY%"
)
if "%MAXY%"=="" (
set sMAXY=
) else (
set sMAXY=-gravity NorthEast -annotate +%g4lLINELEN%+0 "%MAXY%"
)
%IMG7%magick ^
%INFILE% ^
-background %g4lBACKCOL% ^
-pointsize %g4lPNTSZ% ^
-set option:MYSIZE %%wx%%h ^
( -size %%[MYSIZE] xc:%BACKCOL% ^
-draw "line %%[fx:w-1],0,%%[fx:w-1-%g4lLINELEN%],0" ^
-draw "line %%[fx:w-1],%%[fx:h-1],%%[fx:w-1-%g4lLINELEN%],%%[fx:h-1]" ^
%sMINY% ^
%sMAXY% ^
-trim ^
) ^
+swap ^
-gravity Center ^
+append ^
( -size %%[MYSIZE] xc:%g4lBACKCOL% ^
-draw "line 0,0,0,%g4lLINELEN%" ^
-draw "line %%[fx:w-1],0,%%[fx:w-1],%g4lLINELEN%" ^
%sMINX% ^
%sMAXX% ^
-trim ^
) ^
-gravity East ^
-append +repage ^
%OUTFILE%
All images on this page were created by the commands shown, using:
%IMG7%magick -version
Version: ImageMagick 7.1.0-42 Q16-HDRI x64 396d87c:20220709 https://imagemagick.org
Copyright: (C) 1999 ImageMagick Studio LLC
License: https://imagemagick.org/script/license.php
Features: Cipher DPC HDRI OpenCL
Delegates (built-in): bzlib cairo freetype gslib heic jng jp2 jpeg jxl lcms lqr lzma openexr pangocairo png ps raqm raw rsvg tiff webp xml zip zlib
Compiler: Visual Studio 2022 (193231332)
Source file for this web page is logcluts.h1. To re-create this web page, execute "procH1 logcluts".
This page, including the images, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.
Anyone is permitted to re-publish this page, but only for non-commercial use.
Anyone is permitted to link to this page, including for commercial use.
Page version v2.2 5-April-2020.
Page created 24-Aug-2022 21:04:21.
Copyright © 2022 Alan Gibson.















