snibgo's ImageMagick pages

Standard transfer curves

Some standard near-power curves, aka transfer functions, tone or tone response or characteristic curves.

In image processing, we convert between linear (eg scene-referred) luminance levels and non-linear (eg output-referred) values with transfer curves. On this page, "forwards" means from linear to non-linear, and "reverse" means the opposite.

In equations on this page, L is a linear luminance and V is the corresponding non-linear value. Both are in the range [0,1].

For the transfer curves that are not simple power functions, I show a close power function, and the RMSE difference for a grayscale gradient with a flat histogram. An ordinary photograph will usually not have a flat histogram, so we can expect the RMSE difference to be different, and for a particular image a different power curve may be a closer match to the standard function.

Aside: various standards also use these terms:

References

Power curve

The forward equation is:

V = L(1/k)

The reverse equation is:

L = Vk

Commonly, k > 1, so 0 < 1/k < 1. The slopes are then as follows:

direction slope expression slope at 0 slope at 1
forwards dV/dL=(1/k)/L(1-1/k) infinity 1/k
reverse dL/dV=k*V(k-1) 0 k

For example, with k=2.2:

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow %%[fx:1/2.2] ^
  trc_pow.png

call %PICTBAT%graphLineCol ^
  trc_pow.png . 1
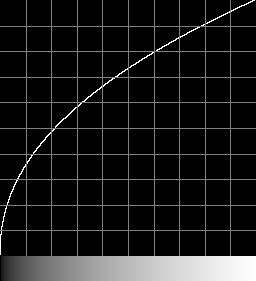
 trc_pow_glc.png

Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow 2.2 ^
  trc_pow_r.png

call %PICTBAT%graphLineCol ^
  trc_pow_r.png . 1
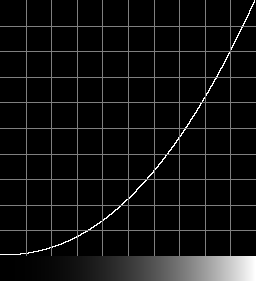
 trc_pow_r_glc.png

A power curve can be used to make mid-tones lighter or darker while leaving black and white unchanged. The greatest change occurs where the curve is parallel to V=L, ie where the slope is 1.0. For example, if k=1.5, the forwards slope is (2/3)/L1/3, so the greatest change is at:

(2/3)/L1/3 = 1

L1/3 = 2/3

L = (2/3)3 
  = 8/27
  = 0.2963

More generally, if y=xp where p>1 then dy/dx=p*x(p-1). When the slope is 1.0 then: 

p*x(p-1) = 1

x(p-1) = 1/p

x = (1/p)(1/(p-1))

Adbobe RGB (1998): a gamma curve

This is a simple power curve with k=2.19921875, which is 2 + 51/256 = 563/256.

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow %%[fx:256/563] ^
  trc_adob.png

call %PICTBAT%graphLineCol ^
  trc_adob.png . 1
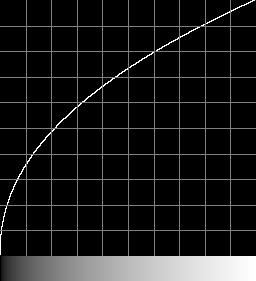
 trc_adob_glc.png

Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow %%[fx:563/256] ^
  trc_adob_r.png

call %PICTBAT%graphLineCol ^
  trc_adob_r.png . 1
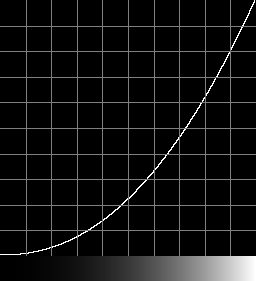
 trc_adob_r_glc.png

The AdobeRGB curve is similar to a power curve with k=2.2. How close are they?

%IMG7%magick compare ^
  -metric RMSE ^
  trc_adob.png trc_pow.png ^
  NULL: 
5.73265 (8.74746e-05)

sRGB: a hybrid linear-gamma

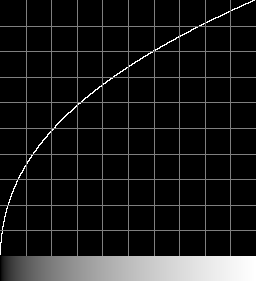
This curve has two components: a linear portion and a power curve.

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -set colorspace RGB ^
  -colorspace sRGB ^
  trc_srgb.png

call %PICTBAT%graphLineCol ^
  trc_srgb.png . 1
 trc_srgb_glc.png

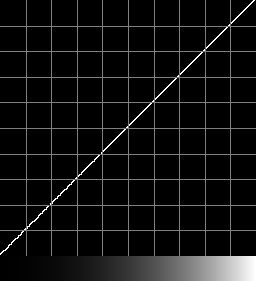
Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -set colorspace sRGB ^
  -colorspace RGB ^
  trc_srgb_r.png

call %PICTBAT%graphLineCol ^
  trc_srgb_r.png . 1
 trc_srgb_r_glc.png

The sRGB curve is similar to a power curve with k=2.2. How close are they?

%IMG7%magick compare ^
  -metric RMSE ^
  trc_srgb.png trc_pow.png ^
  NULL: 
368.807 (0.00562763)

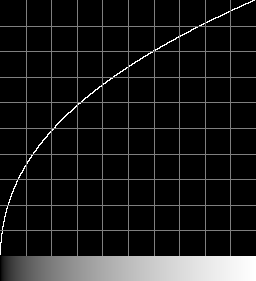
When we have an ICC profile ...

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -profile %ICCPROF%\sRGB-elle-V4-g10.icc ^
  -profile %ICCPROF%\sRGB-elle-V4-srgbtrc.icc ^
  trc_srgbpr.png

call %PICTBAT%graphLineCol ^
  trc_srgbpr.png . 1
 trc_srgbpr_glc.png

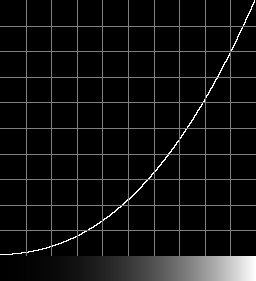
Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -profile %ICCPROF%\sRGB-elle-V4-srgbtrc.icc ^
  -profile %ICCPROF%\sRGB-elle-V4-g10.icc ^
  trc_srgbpr_r.png

call %PICTBAT%graphLineCol ^
  trc_srgbpr_r.png . 1
 trc_srgbpr_r_glc.png

How close is the "-profile" result to the "-colorspace" result?

%IMG7%magick compare ^
  -metric RMSE ^
  trc_srgb.png trc_srgbpr.png ^
  NULL: 
0.433013 (6.60735e-06)

They are practically identical.

L of CIE L*a*b*

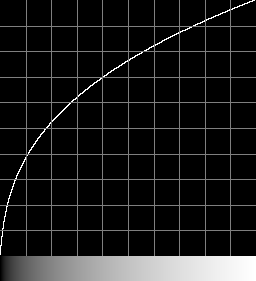
We show the L* channel.

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -set colorspace RGB ^
  -colorspace Lab ^
  -channel 0 -separate +channel ^
  -set colorspace sRGB ^
  trc_lab.png

call %PICTBAT%graphLineCol ^
  trc_lab.png . 1
 trc_lab_glc.png

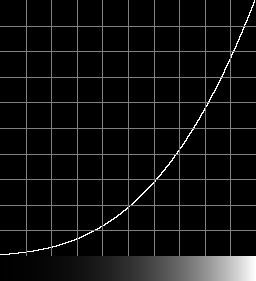
Reverse

%IMG7%magick ^
  -size 256x1 ^
    gradient:Black-White ^
    xc:gray(50%%) ^
    xc:gray(50%%) ^
  -combine ^
  -set colorspace Lab ^
  -colorspace RGB ^
  -set colorspace sRGB ^
  trc_lab_r.png

call %PICTBAT%graphLineCol ^
  trc_lab_r.png . 1
 trc_lab_r_glc.png

The L of Lab curve is similar to a power curve with k=2.68. How close are they?

%IMG7%magick ^
  trc_lab.png ^
  ( -size 256x1 gradient:black-white ^
    -evaluate Pow %%[fx:1/2.68] ^
  ) ^
  -format "%%[distortion]\n" -compare ^
  info: 
0.995638

SMPTE ST 2084

This is also known as the Perceptual Quantizer, PQ.

According to Wikipedia, this transfer curve uses five constants:

c1 = c3 - c2 + 1 = 107/128
c2 = 2413/128
c3 = 2392/128
m1 = 1305/8192
m2 = 2523/32

The forwards transformation is:

P = c1 + c2*L0m1 
    1 + c3*L0m1 

V = Pm2

Note that when L0=0, then V = c1m2 = (107/128)(2523/32), approximately 7.3096e-07. There is no positive L at which V=0.

When L0=1, then P = (c1 + c2) / (1 + c3) = (c3 + 1) / (1 + c3) = 1, so V=1.

Some algebra gives the inverse:

LL = V(1/m2) 

PP =  c1 - LL   
     c3*LL - c2 

L = PP(1/m1)

In the implementation below, both directions are defined only for positive input values. In the reverse transformation, low input values make PP slightly negative, so we have to special-case this.

set c1=0.8359375
set c2=18.8515625
set c3=18.6875
set m1=0.1593017578125
set m2=78.84375

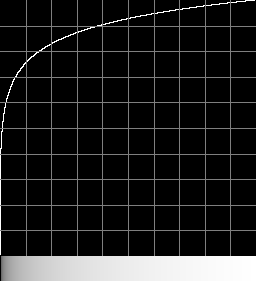
Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -fx "LOM=pow(u,%m1%);PP=(%c1%+%c2%*LOM)/(1+%c3%*LOM);pow(PP,%m2%)" ^
  trc_2084.png

call %PICTBAT%graphLineCol ^
  trc_2084.png . 1
 trc_2084_glc.png

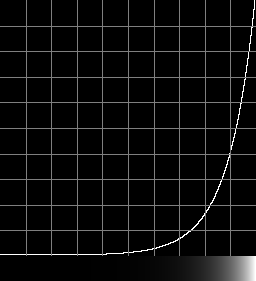
Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -fx "LL=pow(u,1/%m2%);PP=(%c1%-LL)/(%c3%*LL-%c2%);PP<=0?0:pow(PP,1/%m1%)" ^
  trc_2084_r.png

call %PICTBAT%graphLineCol ^
  trc_2084_r.png . 1
 trc_2084_r_glc.png

We can check the round-trip of forwards then reverse:

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  ( +clone ^
    -fx "LOM=pow(u,%m1%);PP=(%c1%+%c2%*LOM)/(1+%c3%*LOM);pow(PP,%m2%)" ^
    -fx "LL=pow(u,1/%m2%);PP=(%c1%-LL)/(%c3%*LL-%c2%);PP<=0?0:pow(PP,1/%m1%)" ^
  ) ^
  -metric RMSE -format %%[distortion] -compare ^
  info: 
9.5719e-08

The round-trip is accurate.

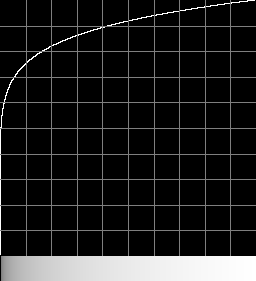
The transformation is fairly close to a power curve with k=8:

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow %%[fx:1/8] ^
  trc_pow8.png

call %PICTBAT%graphLineCol ^
  trc_pow8.png . 1
 trc_pow8_glc.png

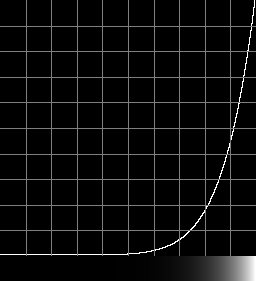
Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow 8 ^
  trc_pow8_r.png

call %PICTBAT%graphLineCol ^
  trc_pow8_r.png . 1
 trc_pow8_r_glc.png

How close?

%IMG7%magick compare ^
  -metric RMSE ^
  trc_2084.png trc_pow8.png ^
  NULL: 
749.514 (0.0114369)

Hybrid log-gamma

This is a gamma curve (ie power curve) at low values, and a log curve at high values. There are three constants:

set a=0.17883277
set b=0.28466892
set c=0.55991073

The forwards transformation is:

When Lc <= 1/12:

    V = sqrt(3) * sqrt(Lc)

When Lc > 1/12:

    V = a * ln(12*Lc - b) + c

The boundary between the two curves is at Lc=1/12,
so V = sqrt(3)*sqrt(Lc) = sqrt(3/12) = sqrt(1/4) = 1/2

Some algebra gives the reverse:

When V <= 1/2:

    Lc = V2/3

When V > 1/2:

    Lc = (exp[(V - c)/a] + b)/12

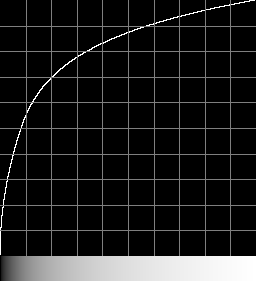
Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -fx "u<=1/12?sqrt(3*u):%a%*ln(12*u-%b%)+%c%" ^
  trc_hlg.png

call %PICTBAT%graphLineCol ^
  trc_hlg.png . 1
 trc_hlg_glc.png

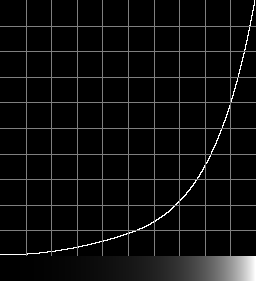
Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -fx "u<=1/2?u*u/3:(exp((u-%c%)/%a%)+%b%)/12" ^
  trc_hlg_r.png

call %PICTBAT%graphLineCol ^
  trc_hlg_r.png . 1
 trc_hlg_r_glc.png

We can check the round-trip of forwards then reverse:

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  ( +clone ^
    -fx "u<=1/12?sqrt(3*u):%a%*ln(12*u-%b%)+%c%" ^
    -fx "u<=1/2?u*u/3:(exp((u-%c%)/%a%)+%b%)/12" ^
  ) ^
  -metric RMSE -format %%[distortion] -compare ^
  info: 
5.67814e-08

The round-trip is accurate.

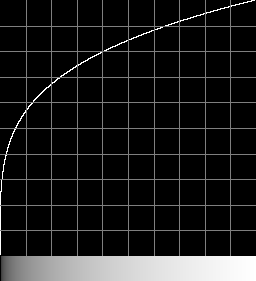
The transformation is not far from a power curve with k=4.0:

Forwards

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow %%[fx:1/4] ^
  trc_pow4x.png

call %PICTBAT%graphLineCol ^
  trc_pow4x.png . 1
 trc_pow4x_glc.png

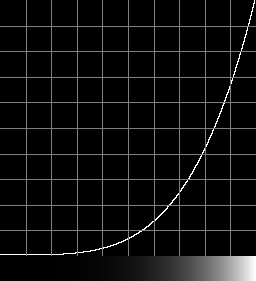
Reverse

%IMG7%magick ^
  -size 256x1 gradient:Black-White ^
  -evaluate Pow 4 ^
  trc_pow4x_r.png

call %PICTBAT%graphLineCol ^
  trc_pow4x_r.png . 1
 trc_pow4x_r_glc.png

How close?

%IMG7%magick compare ^
  -metric RMSE ^
  trc_hlg.png trc_pow4x.png ^
  NULL: 
2423.2 (0.0369756)

This isn't a good approximation, but not too bad.

All images on this page were created by the commands shown, using:

%IMG7%magick -version
Version: ImageMagick 7.1.0-42 Q16-HDRI x64 396d87c:20220709 https://imagemagick.org
Copyright: (C) 1999 ImageMagick Studio LLC
License: https://imagemagick.org/script/license.php
Features: Cipher DPC HDRI OpenCL 
Delegates (built-in): bzlib cairo freetype gslib heic jng jp2 jpeg jxl lcms lqr lzma openexr pangocairo png ps raqm raw rsvg tiff webp xml zip zlib
Compiler: Visual Studio 2022 (193231332)

To improve internet download speeds, some images may have been automatically converted (by ImageMagick, of course) from PNG or TIFF or MIFF to JPG.

Source file for this web page is transcrve.h1. To re-create this web page, execute "procH1 transcrve".

This page, including the images, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.

Anyone is permitted to re-publish this page, but only for non-commercial use.

Anyone is permitted to link to this page, including for commercial use.

Page version v1.0 10-March-2020.

Page created 23-Aug-2022 08:53:52.

Copyright © 2022 Alan Gibson.