call %PICTBAT%tritsttst tri3.txt tri3

Two new features could be added to ImageMagick: -distort Triangulate and -sparse-colour Triangulate.
To my own development version of ImageMagick, I have added a new method to both -distort and -sparse-colour. The method is called Triangulate. It takes any number of control points and triangulates them so the resulting value (displacement or colour) at a pixel depends on at most three control points.
Methods and scripts here are mathematically correct, but may not be arithmetically exact. For example, a point might be very close to (or exactly on) the edge of a circle defined by three other points. Rounding errors can yield the wrong result. For my purposes, this rarely matters.
References:
I am not the first person to write triangulation software. Notable examples include Qhull by C.B. Barber, TetGen by Hang Si, and Triangle by Jonathan Richard Shewchuk.
These come with licences that are more or less restrictive. I wanted C-code that I could use personally use in commercial projects, include it in software that I sold or gave away, and perhaps persuade ImageMagick developers to include it in IM.
The sofware below is my copyright merely to prevent other people claiming copyright on it, preventing me from doing things with it. You can do anything you want with it. Include it in your own projects, commercial or otherwise, distribute it with or without attribution or source code, modify it, correct it, hack it about, anthing you want.
It comes with no guarantees whatsoever.
I have written software such that it can be called from ImageMagick "-sparse-colors triangulate" or "-process triangulate", or from my own C programs.
To call my software from IM's "-sparse-colors", IM source code must be modified. I give the diff files below. This includes #include triangul.inc, so no extra *.c or *.h source files are added to IM. (This doesn't conform to normal IM practice. If my software is incorporated into IM, the developers can do this however they like.)
A point has coordinates. It contains a pointer to one edge in a ring of edges around that point. It doesn't matter which edge of the ring it points to.
An edge joins two points, and is directed from an origin point (org) to a destination point (dst). There are two other pointers. One points to the next counter-clockwise edge in the ring around this edge's origin. The other points to the next counter-clockwise edge in the ring around this edge's destination.
When a new edge is added, it is inserted into two rings: that around the edge's origin, and that around the edge's destination.
What happens if two points are given with the same coordinates? The software might die, or reject all but one of those points, or create a bad triangulation. In the current version, the software exits with a failure, which causes the IM calling program to fail.
A triangulation of the points, not necessarily a Delaunay triangulation, is easy to find. A number of methods can be used, for example:
Code here implements the first two of those methods.
When we have two lines, each defined by end-points, testing whether they intersect is itself quite awkward.
Once a triangulation has been found, it can be converted to a Delaunay triangulation. This code does [i]not[/i] implement Delaunay.
When control points have been triangulated, we calculate for every pixel in the image:
For a smoother result, we can apply a sigmoidal contrast or a power to the barycentric weights.
The barycentric weights are then used to weight the arguments at each vertex, giving the correct arguments for each pixel. (The arguments are a colour for -sparse-color, or delta coordinates for -distort.)
When a pixel is inside the convex hull, it is inside a triangle, and we use the vertex colours and barycentric coordinates to calculate the pixel's colour. What about pixels that are outside the convex hull?
When a pixel falls outside all the triangles, we can find the barycentric coordinates that correspond to each triangle. One or more of these will be outside the range [0..1]. Which triangle should we use? After some experimenting, I chose the following algorithm.
This results in smooth colour gradients outside the convex hull, that look as we might expect.
Each edge on the convex hull is an edge to only one triangle. So the closest edge defines the closest triangle, so we can calculate the barycentric coordinates for that triangle.
Behaviour outside the convex hull can be changed by the attribute triangulate:outside. This may be Extrapolate which uses the calculated barycentric coordinates, Clamp which clamps barycentric coordinates to the range [0..1], or Background which ignores barycentric coordinates and set pixels to the -background colour. See the examples below.
Floating-point arithmetic isn't exact, so it can be incorrect. When a pixel lies on or very close to the edge between two triangles, it can fail the test for being inside either triangle. Two methods of coping with this are:
This software uses the second method.
This could be built as two process modules: one for distortion by triangulation, the other for sparse colours by triangulation. It seems more obvious to add these as methods to "-distort" and "-sparse-color".
See below for diff files. In brief, the changes to standard ImageMagick are:
magick\option.c in DistortOptions[] after Shepards insert line:
{ "Triangulate", TriangulateDistortion, UndefinedOptionFlag, MagickFalse },
In SparseColorOptions[] after Shepards insert line:
{ "Triangulate", TriangulateColorInterpolate, UndefinedOptionFlag, MagickFalse },
magick\distort.h: for typedef DistortImageMethod, add value after ShepardsDistortion, "TriangulateDistortion". for typedef SparseColorMethod, after ShepardsColorInterpolate, add TriangulateColorInterpolate=TriangulateDistortion
magick\distort.c function DistortImage(): add new case TriangulateDistortion similar to case ShepardsDistortion.
magick\distort.c function SparseColorImage(): initialisation code to read the points and triangulate them; within j,i loops add case for new value of sparse_method; wrap-up code to release memory.
The function InitTri() sends text output to stderr. See examples below. Scripts can read this output for data on the triangulation. For example, convTriImg.bat makes annotated images of edges, triangles and the convex hull.
Callers should use three functions and two data structures.
See the source code triangul.inc for more information on the functions and data structures.
For -sparse-colors, there are between one and five arguments per vertex, representing the colour values at the vertex.
For -distort, there are exactly two arguments per vertex, representing the displacement at the vertex: (src.x-dest.x, src.y-dest.y). The vertex coordinates are taken from the destination coordinates, thus the triangulation is of the destination points, not the source points. (distort.c works by walking through the destination pixels, and wants to know the source coordinates from which to get the colour.)
The program tritst.exe (source code tritst.c below) is a simple wrapper program around the software that does the real work: tringul.inc. The program reads from stdin, and writes text data to stderr (following the usual IM convention).
The program is used for development and testing.
The coordinates are shown respecting the "-precision" setting.
We create a text file named tri3.txt. It contains three points, each with two values: the x and y coordinates.
tri3.txt:
3 2 100 0 0 100 300 150
tritst <tri3.txt 2>tri3_output.lis
MinCoord: 0 0
MaxCoord: 300 150
NumPoints: 3
point: 100 0 # 0
first: 0 pts: 0 1
next: 1 pts: 0 2
point: 0 100 # 1
first: 0 pts: 0 1
next: 2 pts: 1 2
point: 300 150 # 2
first: 1 pts: 0 2
next: 2 pts: 1 2
CountedEdges: 6
NumEdges: 3
edge: 100 0 0 100 pts: 0 -1 # 0 numTri: 1 tri: 0
edge: 100 0 300 150 pts: 0 -2 # 1 numTri: 1 tri: 0
edge: 0 100 300 150 pts: -1 -2 # 2 numTri: 1 tri: 0
NumTriangles: 1
trianglePts: 0 2 1 # 0
triangle: 100 0 300 150 0 100
triangleCentXY: 133.333333 83.3333333
The text output lists points (with the edges of each), and the edges and triangles. The lines with "point:", "edge:" and "triangle:" show the coordinates of the associated points, so can be readily used by IM's "-draw" operation.
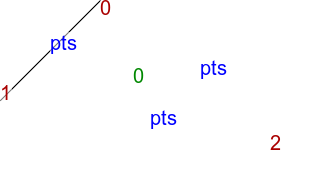
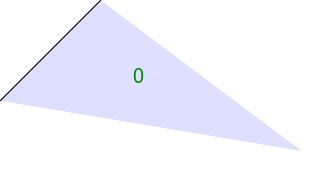
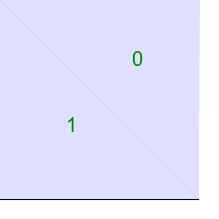
The script tritsttst.bat runs tritst.exe, reads the text output and creates two images. The first image shows points and edges, and numbers each point, edge and triangle. The second image shows all the triangle, colored blue, providing a visual check that all the expected triangles have been found. The third image shows the convex hull of the points, by simply drawing white triangles on a black background.
call %PICTBAT%tritsttst tri3.txt tri3 |



|
tri4.txt:
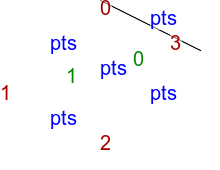
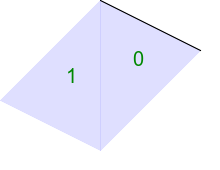
4 2 100 0 0 100 100 150 200 50
call %PICTBAT%tritsttst tri4.txt tri4 |

|
The next example has control points at the corners of the image, so it is fully triangulated.
tri6.txt:
6 2 0 0 299 0 0 149 299 149 100 50 200 100
call %PICTBAT%tritsttst tri6.txt tri6 |
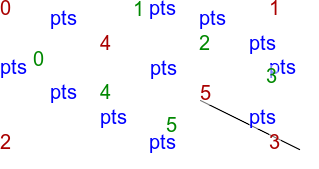
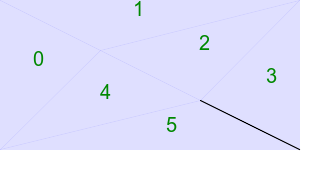

|
We can create random points.
rem call %PICTBAT%mRandPts ^ rem triRnd100.txt 600 400 100 3 call %PICTBAT%tritsttst ^ triRnd100.txt triRnd100 |

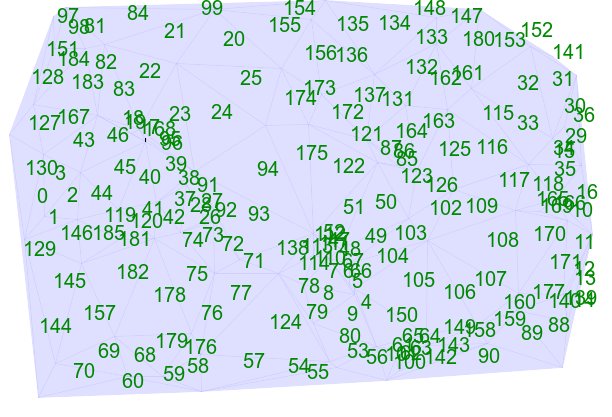
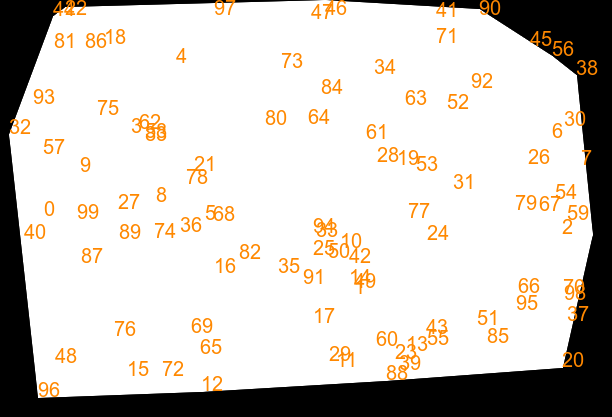
|
tritst.exe exercises the barycentric calculation, sending results to stdout.
tri3v.txt:
3 3 2 0 0.1 0 2 0.5 6 3 1.0
tritst <tri3v.txt >tri3v.lis
Reading 3 points each with 3 arguments. Call InitTri TriangulateSrtEdge start TriangulateSrtEdge 1 TriangulateSrtEdge 2 TriangulateSrtEdge 3 TriangulateSrtEdge 4 TriangulateSrtEdge end Triangles: T=2 AddTriangles p0!=p3 or neg area dt pts 0 1 2 0 AreaX2=-14 triPts: 0 2 1 # 0 tri: 2 0 6 3 0 2 A=7 CntTri: 1 Integrity check of st: 3 edges: 0 1 1 1 2 1 Finished InitTri 0 0 RV: 0.0142857 1 0 RV: 0.0571429 2 0 RV: 0.1 3 0 RV: 0.142857 4 0 RV: 0.185714 5 0 RV: 0.228571 6 0 RV: 0.271429 7 0 RV: 0.314286 8 0 RV: 0.357143 9 0 RV: 0.4 0 1 RV: 0.257143 1 1 RV: 0.3 2 1 RV: 0.342857 3 1 RV: 0.385714 4 1 RV: 0.428571 5 1 RV: 0.471429 6 1 RV: 0.514286 7 1 RV: 0.557143 8 1 RV: 0.6 9 1 RV: 0.642857 0 2 RV: 0.5 1 2 RV: 0.542857 2 2 RV: 0.585714 3 2 RV: 0.628571 4 2 RV: 0.671429 5 2 RV: 0.714286 6 2 RV: 0.757143 7 2 RV: 0.8 8 2 RV: 0.842857 9 2 RV: 0.885714 0 3 RV: 0.742857 1 3 RV: 0.785714 2 3 RV: 0.828571 3 3 RV: 0.871429 4 3 RV: 0.914286 5 3 RV: 0.957143 6 3 RV: 1 7 3 RV: 1.04286 8 3 RV: 1.08571 9 3 RV: 1.12857 0 4 RV: 0.985714 1 4 RV: 1.02857 2 4 RV: 1.07143 3 4 RV: 1.11429 4 4 RV: 1.15714 5 4 RV: 1.2 6 4 RV: 1.24286 7 4 RV: 1.28571 8 4 RV: 1.32857 9 4 RV: 1.37143 0 5 RV: 1.22857 1 5 RV: 1.27143 2 5 RV: 1.31429 3 5 RV: 1.35714 4 5 RV: 1.4 5 5 RV: 1.44286 6 5 RV: 1.48571 7 5 RV: 1.52857 8 5 RV: 1.57143 9 5 RV: 1.61429 0 6 RV: 1.47143 1 6 RV: 1.51429 2 6 RV: 1.55714 3 6 RV: 1.6 4 6 RV: 1.64286 5 6 RV: 1.68571 6 6 RV: 1.72857 7 6 RV: 1.77143 8 6 RV: 1.81429 9 6 RV: 1.85714 0 7 RV: 1.71429 1 7 RV: 1.75714 2 7 RV: 1.8 3 7 RV: 1.84286 4 7 RV: 1.88571 5 7 RV: 1.92857 6 7 RV: 1.97143 7 7 RV: 2.01429 8 7 RV: 2.05714 9 7 RV: 2.1 0 8 RV: 1.95714 1 8 RV: 2 2 8 RV: 2.04286 3 8 RV: 2.08571 4 8 RV: 2.12857 5 8 RV: 2.17143 6 8 RV: 2.21429 7 8 RV: 2.25714 8 8 RV: 2.3 9 8 RV: 2.34286 0 9 RV: 2.2 1 9 RV: 2.24286 2 9 RV: 2.28571 3 9 RV: 2.32857 4 9 RV: 2.37143 5 9 RV: 2.41429 6 9 RV: 2.45714 7 9 RV: 2.5 8 9 RV: 2.54286 9 9 RV: 2.58571
Test: what happens to 4 or more colinear points? The code in distort.c will fall back to Shepards.
tricolin4.txt:
4 2 0 0 10 10 20 20 30 30
tritst <tricolin4.txt 2>tri_colin4.lis
This outputs tri_colin4.lis:
MinCoord: 0 0
MaxCoord: 30 30
NumPoints: 4
point: 0 0 # 0
first: 0 pts: 0 1
point: 10 10 # 1
first: 0 pts: 0 1
next: 1 pts: 1 2
point: 20 20 # 2
first: 1 pts: 1 2
next: 2 pts: 2 3
point: 30 30 # 3
first: 2 pts: 2 3
CountedEdges: 6
NumEdges: 3
edge: 0 0 10 10 pts: 0 -1 # 0 numTri: 0 tri: null
edge: 10 10 20 20 pts: -1 -2 # 1 numTri: 0 tri: null
edge: 20 20 30 30 pts: -2 -3 # 2 numTri: 0 tri: null
NumTriangles: 0
The triangulation has found edges but no triangles, so the points must be colinear.
The triangulation of points (angular distance INTVL degrees) arranged in a circle (radius RAD pixels) looks like this:
set RAD=200
set INTVL=10
set /A NUM=360/%INTVL%
echo %NUM% 2 >tri_circ.lis
(for /L %%i in (0,%INTVL%,359) do @(
@%IM%identify ^
-format "%%[fx:%RAD%+int(%RAD%*sin(%%i*3.1415926/180)+0.5)] %%[fx:%RAD%+int(%RAD%*cos(%%i*3.1415926/180)+0.5)]\n" ^
xc:
)) >>tri_circ.lis
call %PICTBAT%tritsttst tri_circ.lis tri_circ_out
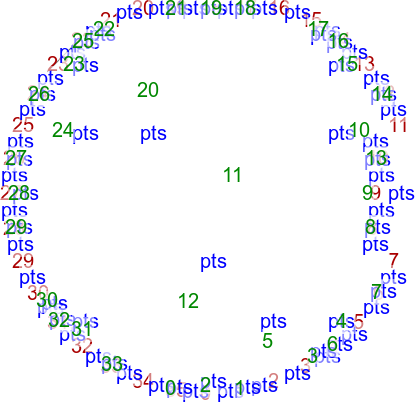
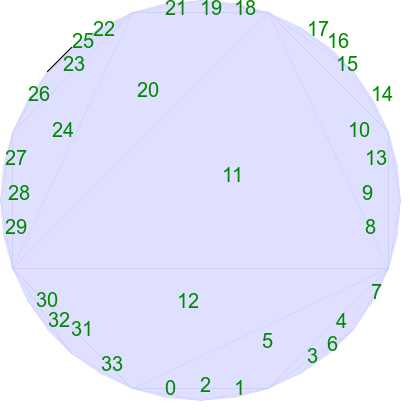

|
The triangulation of points arranged in a rectangle looks like this:
set INTVL=50 echo 40 2 >tri_rect.lis (for /L %%i in (0,1,12) do @( @set /A X=%INTVL%*%%i @echo !X! 0 @echo !X! 400 )) >>tri_rect.lis (for /L %%i in (1,1,7) do @( @set /A Y=%INTVL%*%%i @echo 0 !Y! @echo 600 !Y! )) >>tri_rect.lis call %PICTBAT%tritsttst tri_rect.lis tri_rect_out
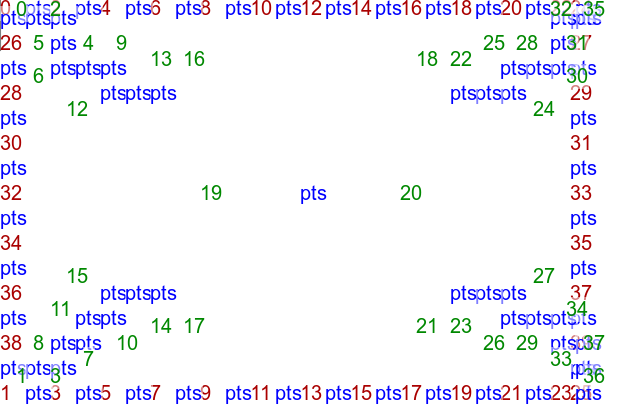
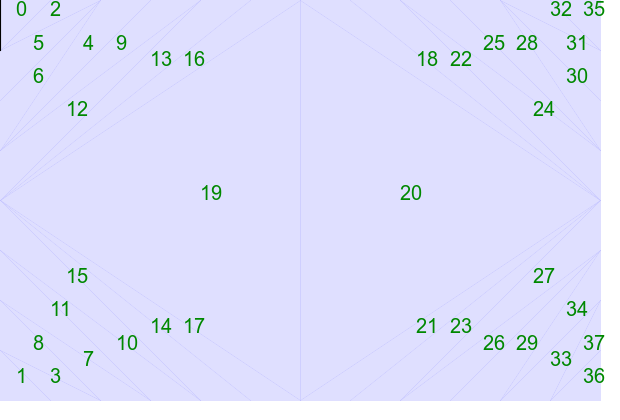
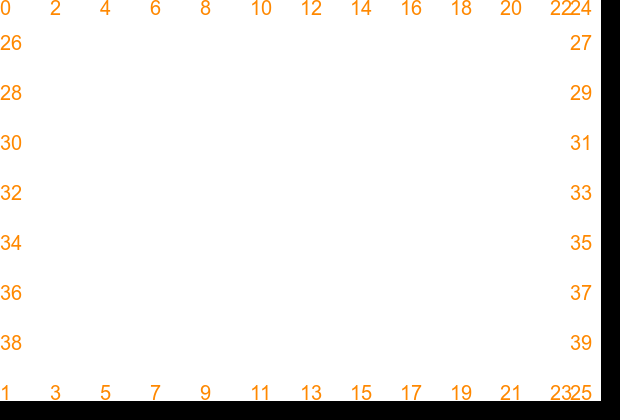
|
That concludes the demonstration of tritst.exe, a shell program around triangul.h.
set RAD=200
set INTVL=10
set /A NUM=360/%INTVL%
set /A NUMp1=%NUM%+1
echo %NUMp1% 2
(for /L %%i in (0,%INTVL%,359) do @(
@%IM%identify ^
-format "%%[fx:%RAD%+int(%RAD%*sin(%%i*3.1415926/180)+0.5)] %%[fx:%RAD%+int(%RAD%*cos(%%i*3.1415926/180)+0.5)]\n" ^
xc:
))
echo %RAD% %RAD%
call %PICTBAT%tritstlasttst tri_clck.lis tri_clck_out
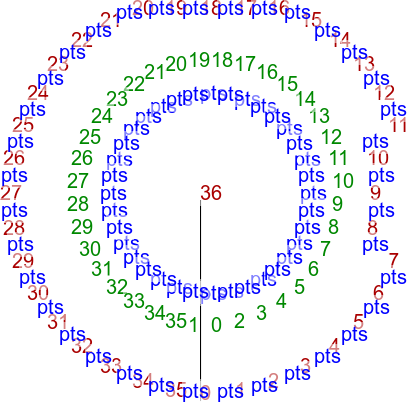
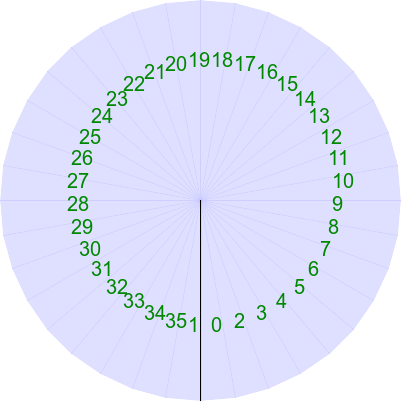

|
set INTVL=50 echo 41 2 >tri_rectclk.lis (for /L %%i in (0,1,12) do @( @set /A X=%INTVL%*%%i @echo !X! 0 @echo !X! 400 )) >>tri_rectclk.lis (for /L %%i in (1,1,7) do @( @set /A Y=%INTVL%*%%i @echo 0 !Y! @echo 600 !Y! )) >>tri_rectclk.lis @echo 300 200 >>tri_rectclk.lis call %PICTBAT%tritstlasttst tri_rectclk.lis tri_rectclk_out
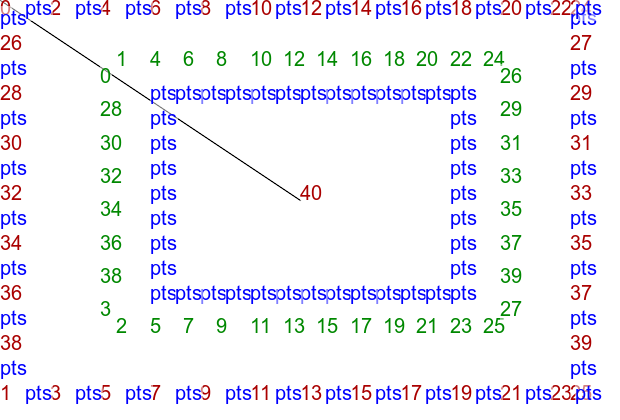
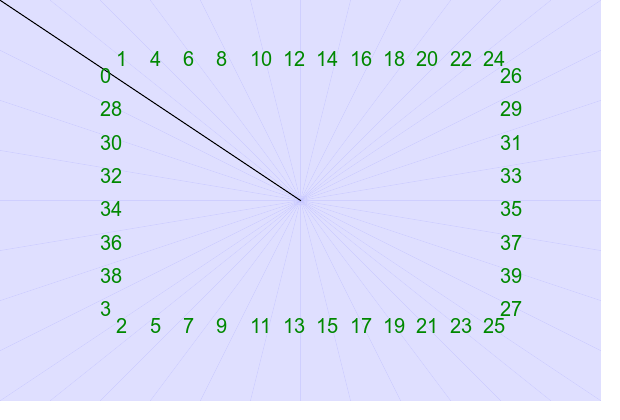

|
The main point of triangul.h is to integrate it into ImageMagick. It provides a new method for both -sparse-color (described here) and -distort (described in a section below).
Like other -sparse-color methods, it takes a list of control points, where each control point has three elements: x-coordinate, y-coordinate and a colour. The coordinates can be floating-point. My code imposes no limit on the number of control points, but for performance reasons one thousand is a sensible limit.
|
convTriImg needs a verbose output from -sparse-color Triangulate. %IMDEV%convert ^
-verbose ^
-size 300x200 xc: ^
-sparse-color Triangulate ^
100,0,rgb(0,0,50%%),0,100,rgb(50%%,0,0),100,150,rgb(50%%,0,50%%),200,50,rgb(0,50%%,0) ^
tri_col3.png >tri_col3.lis 2^>^&1
|

|
call %PICTBAT%convTriImg tri_col3.lis tri_col3 |
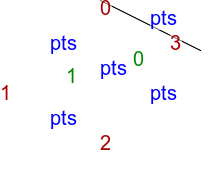
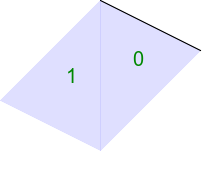

|
|
Using "Voronoi" instead of "Triangulate" provides a different view of the control points: %IMDEV%convert ^
-size 300x200 xc: ^
-sparse-color Voronoi ^
100,0,rgb(0,0,50%%),0,100,rgb(50%%,0,0),100,150,rgb(50%%,0,50%%),200,50,rgb(0,50%%,0) ^
tri_vor3.png
|

|
The images made by convTriImg.bat can be composited over the created image, using gravity NorthWest. We clearly see the green has been extrapolated outside the convex hull, becoming lighter and more saturated.
%IMDEV%convert ^ tri_col3.png ^ tri_col3_l.png ^ -gravity NorthWest -composite ^ tri_col3_comp.png |
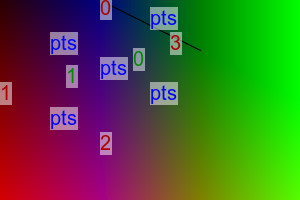
|
Instead of writing the coordinates and colours every time, we can put them in a text file, eg tri4p.txt:
100,0,rgb(0,0,50%%), 0,100,rgb(50%%,0,0), 100,150,rgb(50%%,0,50%%), 200,50,rgb(0,50%%,0)
%IMDEV%convert ^ -size 300x200 xc: ^ -sparse-color Triangulate "@tri4p.txt" ^ tri_4p.png |

|
Test short edge and long edge:
%IMDEV%convert ^
-verbose ^
-size 300x200 xc: ^
-sparse-color Triangulate ^
100,0,rgb(0,0,50%%),80,150,rgb(50%%,0,0),100,150,rgb(50%%,0,50%%),200,50,rgb(0,50%%,0) ^
tri_col3a.png >tri_col3a.lis 2^>^&1
|

|
call %PICTBAT%convTriImg tri_col3a.lis tri_col3a |
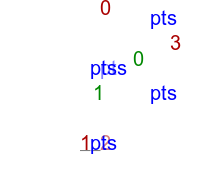
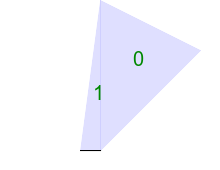

|
Gradient with skewed center, where triskewc.txt is:
0,0,white 299,0,white 0,199,black 299,199,black 200,50,gray50
%IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -sparse-color Triangulate "@triskewc.txt" ^ tri_skewc.png >tri_skewc.lis 2^>^&1 There appear to be four dark lines from the corners,
|

|
call %PICTBAT%convTriImg tri_skewc.lis tri_skewc |
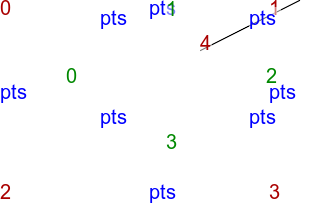
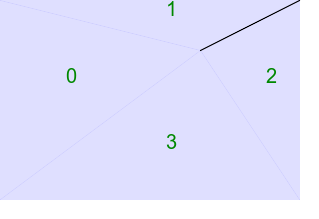
|
|
We can show the contours of the result. %IM%convert ^
tri_skewc.png ^
( -size 1x500 gradient: -rotate 90 ^
-duplicate 10 +append ) ^
-clut ^
-morphology edgein diamond:1 ^
tri_skewc_cont.png
|
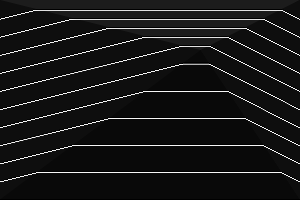
|
For convenience, I put the code that makes contours in an environment variable.
set CONTOUR= ^
( -size 1x500 gradient: -rotate 90 ^
-duplicate 10 +append ) ^
-clut ^
-morphology edgein diamond:1
Compare this with "-sparse-color Shepards":
%IMDEV%convert ^ -size 300x200 xc: ^ -sparse-color Shepards "@triskewc.txt" ^ +write tri_skewsh.png ^ %CONTOUR% ^ tri_skewsh_cont.png |


|
When triangulating, the output can be very sensitive to the position of the control points.
|
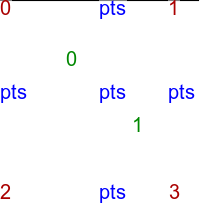
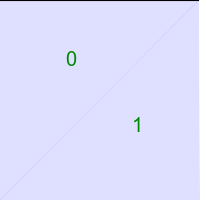
Control points in very nearly a square, but with the top-right point shifted left. %IMDEV%convert ^
-verbose ^
-size 200x200 xc: ^
-sparse-color Triangulate ^
0,0,red,198,0,blue,0,199,blue,199,199,red ^
tri_sq1.png >tri_sq1.lis 2^>^&1
|

|
call %PICTBAT%convTriImg tri_sq1.lis tri_sq1 |

|
|
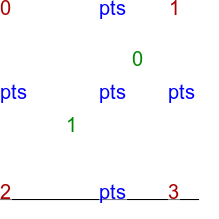
Control points in very nearly a square, but with the bottom-right point shifted left. %IMDEV%convert ^
-verbose ^
-size 200x200 xc: ^
-sparse-color Triangulate ^
0,0,red,199,0,blue,0,199,blue,198,199,red ^
tri_sq2.png >tri_sq2.lis 2^>^&1
|

|
call %PICTBAT%convTriImg tri_sq2.lis tri_sq2 |

|
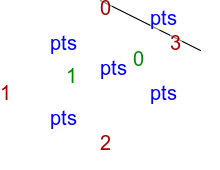
The attribute triangulate:outside determines the the calculation for pixels that are not in any triangle (ie that are outside the convex hull). It can take one of three values.
%IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -background khaki ^ -sparse-color Triangulate "@tri4p.txt" ^ tri_extr.png >tri_extr.lis 2^>^&1 call %PICTBAT%convTriImg tri_extr.lis tri_extr |

|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:outside=clamp ^ -sparse-color Triangulate "@tri4p.txt" ^ tri_clamp.png |

|
%IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -background khaki ^ -define triangulate:outside=background ^ -sparse-color Triangulate "@tri4p.txt" ^ tri_back.png |

|
|
For background "none", we need "-alpha set -channel RGBA". %IMDEV%convert ^ -size 300x200 xc: ^ -background none ^ -alpha set -channel RGBA ^ -define triangulate:outside=background ^ -sparse-color Triangulate "@tri4p.txt" ^ tri_none.png |
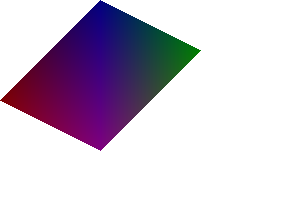
|
If less than three points are given, no triangles can be made, so the method falls back to barycentric.
|
One control point. %IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -sparse-color Triangulate "50 100 #800" ^ tri_1cp.png >tri_1cp.lis 2^>^&1 xc:=> XC 300x200 300x200+0+0 32-bit sRGB 0.000u 0:00.000 Barycentric Sparse Color: -channel R -fx '+0.000000*i +0.000000*j +0.533333' \ -channel G -fx '+0.000000*i +0.000000*j +0.000000' \ -channel B -fx '+0.000000*i +0.000000*j +0.000000' \ xc:=>tri_1cp.png XC 300x200 300x200+0+0 8-bit sRGB 2c 295B 0.125u 0:00.127 |

|
|
Two control points. %IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -sparse-color Triangulate "50,100 #800 100,120 #080" ^ tri_2cp.png >tri_2cp.lis 2^>^&1 xc:=> XC 300x200 300x200+0+0 32-bit sRGB 0.000u 0:00.002 Barycentric Sparse Color: -channel R -fx '-0.009195*i -0.003678*j +1.360920' \ -channel G -fx '+0.009195*i +0.003678*j -0.827586' \ -channel B -fx '+0.000000*i +0.000000*j +0.000000' \ xc:=>tri_2cp.png XC 300x200 300x200+0+0 16-bit sRGB 3.44KB 0.125u 0:00.149 |

|
When there are at least three control points but they are colinear, the method falls back to shepards.
trinlycol4c.txt has control points that are nearly colinear, but not quite:
50 100 #800 100 120 #080 150 130 #008 200 160 #808
tricolin4c.txt has colinear control points:
50 100 #800 100 120 #080 150 140 #008 200 160 #808
|
Control points are nearly colinear. %IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -sparse-color Triangulate "@trinlycol4.txt" ^ tri_nlycol4.png >tri_nlycol4.lis 2^>^&1 Pixels outside the convex hull have barycentic coordinates massively outside [0..1].
|

|
|
Pixels outside the convex hull have barycentic coordinates clamped to [0..1]. %IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -define triangulate:outside=clamp ^ -sparse-color Triangulate "@trinlycol4.txt" ^ tri_nlycol4cl.png |

|
|
Control points are exactly colinear. The method falls back to Shepards. %IMDEV%convert ^ -verbose ^ -size 300x200 xc: ^ -sparse-color Triangulate "@tricolin4c.txt" ^ tri_colin4c.png >tri_colin4c.lis 2^>^&1 |

|
xc:=> XC 300x200 300x200+0+0 32-bit sRGB 0.000u 0:00.002
MinCoord: 50 100
MaxCoord: 200 160
NumPoints: 4
point: 50 100 # 0
first: 0 pts: 0 1
point: 100 120 # 1
first: 0 pts: 0 1
next: 1 pts: 1 2
point: 150 140 # 2
first: 1 pts: 1 2
next: 2 pts: 2 3
point: 200 160 # 3
first: 2 pts: 2 3
CountedEdges: 6
NumEdges: 3
edge: 50 100 100 120 pts: 0 -1 # 0 numTri: 0 tri: null
edge: 100 120 150 140 pts: -1 -2 # 1 numTri: 0 tri: null
edge: 150 140 200 160 pts: -2 -3 # 2 numTri: 0 tri: null
NumTriangles: 0
xc:=>tri_colin4c.png XC 300x200 300x200+0+0 16-bit sRGB 225KB 0.172u 0:00.197
TriangulateDistortion arguments: 50 100 0.533333 0 0 100 120 0 0.533333 0 150 140 0 0 0.533333 200 160 0.533333 0 0.533333
SparseColorImage triangulate number_arguments=20 number_colors=3
SparseTri.NumPoints = 4
SparseTri.NumArgsPp = 5
SparseTri.sigContrast = 0
SparseTri.sigMidpoint = 0.5
SparseTri.power = 1
Arguments: 50 100 0.533333 0 0 100 120 0 0.533333 0 150 140 0 0 0.533333 200 160 0.533333 0 0.533333
TriangulateSrtEdge start
TriangulateSrtEdge 1
TriangulateSrtEdge 2
TriangulateSrtEdge 0 and 1 intersect at segment
TriangulateSrtEdge 0 and 2 intersect at segment
TriangulateSrtEdge 3 and 4 intersect at segment
TriangulateSrtEdge 3
TriangulateSrtEdge 4
TriangulateSrtEdge end
Triangles:
T=1
AddTriangles p0!=p3 or neg area dt pts 0 1 2 3
AddTriangles p0!=p3 or neg area dt pts 1 2 3 2
CntTri: 0
Triangulate: no triangles; possibly colinear points
For pixels inside a triangle, the barycentric coordintes are in the range 0.0 to 1.0, varying linearly from 1.0 at a vertex to 0.0 at the opposite edge. This can be adjusted by a sigmoidal function, which has the same effect on the barycentric coordinates as the IM operator "-sigmoidal-contrast" has on pixel values.
This has no effect on the triangulation; it merely "pushes" the colours towards the triangle vertices, or "pulls" them towards the centre.
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:sigmoidal=1,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsig1.png ^ %CONTOUR% ^ tri_skewsig1_cont.png |


|
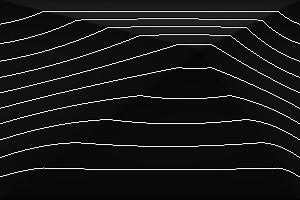
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:sigmoidal=3,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsig3.png ^ %CONTOUR% ^ tri_skewsig3_cont.png |

|
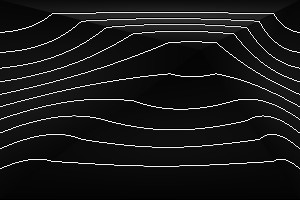
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:sigmoidal=5,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsig5.png ^ %CONTOUR% ^ tri_skewsig5_cont.png |

|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:sigmoidal=10,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsig10.png ^ %CONTOUR% ^ tri_skewsig10_cont.png |


|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:sigmoidal=20,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsig20.png ^ %CONTOUR% ^ tri_skewsig20_cont.png |


|
With an approriate value for contrast (triangulate:sigmoidal=3,50%), the contours have nearly continuous slope, which removes the Mach bands.
We can use an inverse sigmoidal function:
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:invsigmoidal=1,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsigi1.png ^ %CONTOUR% ^ tri_skewsigi1_cont.png |

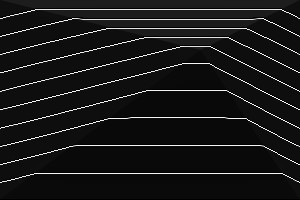
|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:invsigmoidal=3,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsigi3.png ^ %CONTOUR% ^ tri_skewsigi3_cont.png |

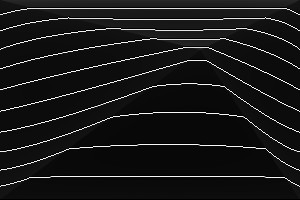
|
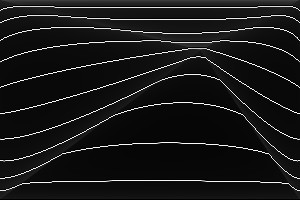
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:invsigmoidal=5,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsigi5.png ^ %CONTOUR% ^ tri_skewsigi5_cont.png |

|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:invsigmoidal=10,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsigi10.png ^ %CONTOUR% ^ tri_skewsigi10_cont.png |


|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:invsigmoidal=20,50%% ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_skewsigi20.png ^ %CONTOUR% ^ tri_skewsigi20_cont.png |


|
The non-inverted form increases contrast in the centre of triangles, lowering contrast around the vertices. For large values of contrast, this creates flat colour around each vertex, with sharp transitions within the triangles.
The inverted form decreases contrast in the centre of triangles, increasing contrast around the vertices. For large values of contrast, this creates flat colour within each triangle, with sharp transitions at the edges.
We can apply a power function to the barycentric coordinates.
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=2 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow1.png ^ %CONTOUR% ^ tri_pow1_cont.png |


|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=1.5 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow2.png ^ %CONTOUR% ^ tri_pow2_cont.png |

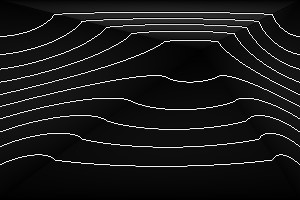
|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=1.1 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow3.png ^ %CONTOUR% ^ tri_pow3_cont.png |


|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=1 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow4.png ^ %CONTOUR% ^ tri_pow4_cont.png |

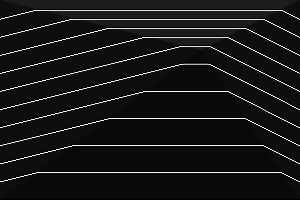
|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=0.9 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow5.png ^ %CONTOUR% ^ tri_pow5_cont.png |

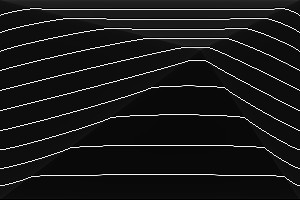
|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=0.75 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow6.png ^ %CONTOUR% ^ tri_pow6_cont.png |

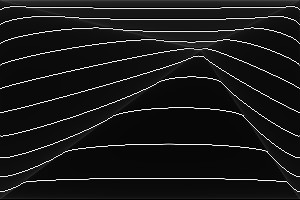
|
%IMDEV%convert ^ -size 300x200 xc: ^ -define triangulate:power=0.5 ^ -sparse-color Triangulate "@triskewc.txt" ^ +write tri_pow7.png ^ %CONTOUR% ^ tri_pow7_cont.png |


|
We can make a hexagonal chart of colours:
0 174 #f00 100 348 #ff0 300 348 #0f0 400 174 #0ff 300 0 #00f 100 0 #f0f 200 174 #888
%IMDEV%convert ^ -size 401x349 xc: ^ -sparse-color Triangulate "@trihex.txt" ^ tri_hex.png |

|
%IMDEV%convert ^ -size 401x349 xc: ^ -background khaki ^ -define triangulate:outside=background ^ -sparse-color Triangulate "@trihex.txt" ^ tri_hex2.png |

|
%IMDEV%convert ^ -size 401x349 xc: ^ -background khaki ^ -define triangulate:invsigmoidal=3,50%% ^ -define triangulate:outside=background ^ -sparse-color Triangulate "@trihex.txt" ^ tri_hex3.png |

|
Make a sample image.
set SRC=tri_dist_src.png call %PICTBAT%grid 300 200 16 16 1 #f00 none #f00 %TEMP%\g.png %IM%convert ^ -size 300x200 gradient:#88f-#8f8 ^ %TEMP%\g.png ^ -composite ^ %SRC% |
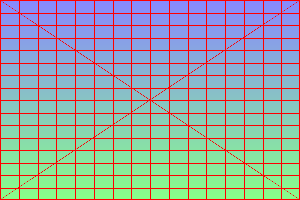
|
Trial:
%IMDEV%convert ^ -verbose ^ %SRC% ^ -distort Triangulate "10,10,12,13 40,41,43,44 20,0,22,0" ^ tri_dis1.png >tri_dis1.lis 2^>^&1 |

|
tri_dist_src.png PNG 300x200 300x200+0+0 16-bit sRGB 14.8KB 0.000u 0:00.006
MinCoord: 12 0
MaxCoord: 43 44
NumPoints: 3
point: 12 13 # 0
first: 0 pts: 0 2
next: 1 pts: 0 1
point: 43 44 # 1
first: 1 pts: 0 1
next: 2 pts: 1 2
point: 22 0 # 2
first: 0 pts: 0 2
next: 2 pts: 1 2
CountedEdges: 6
NumEdges: 3
edge: 12 13 22 0 pts: 0 -2 # 0 numTri: 1 tri: 0
edge: 12 13 43 44 pts: 0 -1 # 1 numTri: 1 tri: 0
edge: 43 44 22 0 pts: -1 -2 # 2 numTri: 1 tri: 0
NumTriangles: 1
trianglePts: 0 2 1 # 0
triangle: 12 13 22 0 43 44
triangleCentXY: 25.6667 19
tri_dist_src.png=>tri_dis1.png PNG 300x200 300x200+0+0 16-bit sRGB 209KB 0.078u 0:00.096
TriangulateDistortion arguments: 10 10 12 13 40 41 43 44 20 0 22 0
DistortImage triangulate number_arguments=12
SparseTri.NumPoints = 3
SparseTri.NumArgsPp = 4
SparseTri.sigContrast = 0
SparseTri.sigMidpoint = 0.5
SparseTri.power = 1
Arguments: 10 10 12 13 40 41 43 44 20 0 22 0
TriangulateSrtEdge start
TriangulateSrtEdge 1
TriangulateSrtEdge 2
TriangulateSrtEdge 3
TriangulateSrtEdge 4
TriangulateSrtEdge end
Triangles:
T=2
triPts: 0 2 1 # 0
tri: 12 13 22 0 43 44 A=356.5
AddTriangles p0!=p3 or neg area dt pts 0 1 2 0 AreaX2=-713
CntTri: 1
Integrity check of st: 3 edges:
0 1
1 1
2 1
%IMDEV%convert ^
-verbose ^
%SRC% ^
-virtual-pixel None ^
-distort Triangulate ^
"10,10,12,13 40,41,43,44 20,0,22,0" ^
tri_dis2.png >tri_di21.lis 2^>^&1
|

|
|
Pin the four corners while displacing the center. %IMDEV%convert ^
%SRC% ^
-distort Triangulate ^
"0,0,0,0 299,0,299,0 0,199,0,199 299,199,299,199 150,100,200,50" ^
tri_dis3.png
|
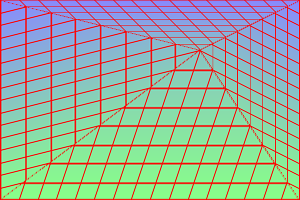
|
|
Compare with the Shepards distortion using the same coordinates: %IMDEV%convert ^
%SRC% ^
-virtual-pixel None ^
-distort Shepards ^
"0,0,0,0 299,0,299,0 0,199,0,199 299,199,299,199 150,100,200,50" ^
tri_shep.png
|

|
|
Apply an inverse sigmoidal. %IMDEV%convert ^
%SRC% ^
-define triangulate:invsigmoidal=6,50%% ^
-distort Triangulate ^
"0,0,0,0 299,0,299,0 0,199,0,199 299,199,299,199 150,100,200,50" ^
tri_dis5.png
|
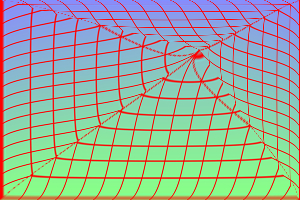
|
|
Power 1.4. %IMDEV%convert ^
%SRC% ^
-define triangulate:power=1.4 ^
-distort Triangulate ^
"0,0,0,0 299,0,299,0 0,199,0,199 299,199,299,199 150,100,200,50" ^
tri_dispow1.png
|
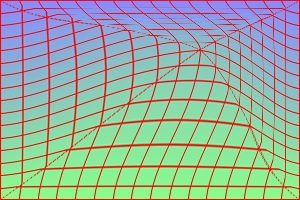
|
|
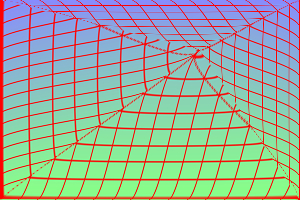
Power 0.7. %IMDEV%convert ^
%SRC% ^
-define triangulate:power=0.7 ^
-distort Triangulate ^
"0,0,0,0 299,0,299,0 0,199,0,199 299,199,299,199 150,100,200,50" ^
tri_dispow2.png
|
|
|
Copy-paste an arbitrary convex polygon, distorting it. %IMDEV%convert ^
%SRC% ^
-define triangulate:outside=background ^
-distort Triangulate ^
"125,50,225,20 100,125,200,150 190,100,270,125" ^
tri_dis6.png
|

|
|
Copy-paste the same convex polygon, extrapolating outside the polygon. %IMDEV%convert ^
%SRC% ^
-define triangulate:outside=extrapolate ^
-distort Triangulate ^
"125,50,225,20 100,125,200,150 190,100,270,125" ^
tri_dis7.png
|

|
|
As our polygon is simply a triangle, extrapolating is equivalent to an affine transformation. %IMDEV%convert ^
%SRC% ^
-distort Affine ^
"125,50,225,20 100,125,200,150 190,100,270,125" ^
tri_aff7.png
|

|
|
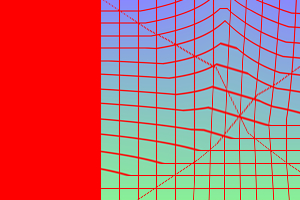
Copy-paste the same convex polygon, clamping outside the polygon. %IMDEV%convert ^
%SRC% ^
-define triangulate:outside=clamp ^
-distort Triangulate ^
"125,50,225,20 100,125,200,150 190,100,270,125" ^
tri_dis8.png
|
|
|
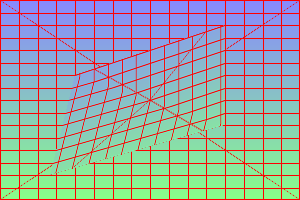
Copy-paste a rectangle. %IMDEV%convert ^
%SRC% ^
-virtual-pixel None ^
-define triangulate:outside=background ^
-distort Triangulate ^
"50,50,75,75 250,50,225,25 50,150,50,175 250,150,225,125" ^
tri_d4_1.png
|
|
|
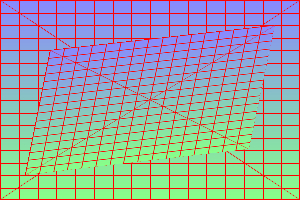
Copy-paste another rectangle. %IMDEV%convert ^
%SRC% ^
-virtual-pixel None ^
-define triangulate:outside=background ^
-distort Triangulate ^
"0,0,50,50 299,0,275,25 0,199,25,175 299,199,249,149" ^
tri_d4_2.png
|
|
If we use %[fx:...] as coordinates, we don't need to edit them for different image sizes. This makes the string long, and awkward to edit and view. Sadly, this doesn't seem to work when we put them in a text file. Instead, we can put them in an environment variable.
For example, we pin the four corners, and shift the center up and right.
set DISP_STR=^ 0,0,0,0,^ %%[fx:w-1],0,%%[fx:w-1],0,^ 0,%%[fx:h-1],0,%%[fx:h-1],^ %%[fx:w-1],%%[fx:h-1],%%[fx:w-1],%%[fx:h-1],^ %%[fx:w/2],%%[fx:h/2],%%[fx:w/2+w/6],%%[fx:h/2-h/4] %IMDEV%convert ^ %SRC% ^ -distort Triangulate "%DISP_STR%" ^ tri_fx1.png |
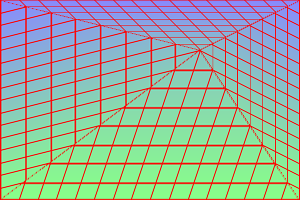
|
If we pin coordinates but apply a sigmoid, the image is unchanged. This is because displacement of pixels within a triangle depends on displacement of the three vertices. If none of the vertices are displaced, neither will any pixel within the triangle be displaced.
set DISP_STR=^ 0,0,0,0,^ %%[fx:w-1],0,%%[fx:w-1],0,^ 0,%%[fx:h-1],0,%%[fx:h-1],^ %%[fx:w-1],%%[fx:h-1],%%[fx:w-1],%%[fx:h-1],^ %%[fx:w/2],%%[fx:h/2],%%[fx:w/2],%%[fx:h/2] %IMDEV%convert ^ %SRC% ^ -distort Triangulate "%DISP_STR%" ^ tri_fx2.png |

|
We can place the source on a canvas of twice the dimensions (using -extent), and expand the image outwards by moving the source corners to the entended corners. This would be the same as -resize but we also apply a sigmoidal. The creates an "implode" effect. We can distort the expansion with sigmoidal or power (or both).
|
With no sigmoidal or power, the effect is the same as "-resize". set DISP_STR=^ %%[fx:w/4],%%[fx:h/4],0,0,^ %%[fx:w*3/4],%%[fx:h/4],%%[fx:w-1],0,^ %%[fx:w/4],%%[fx:h*3/4],0,%%[fx:h-1],^ %%[fx:w*3/4],%%[fx:h*3/4],%%[fx:w-1],%%[fx:h-1],^ %%[fx:w/2],%%[fx:h/2],%%[fx:w/2],%%[fx:h/2] %IMDEV%convert ^ %SRC% ^ -gravity Center -extent 200%% ^ -distort Triangulate "%DISP_STR%" ^ -resize 50%% ^ tri_dimp0.png |
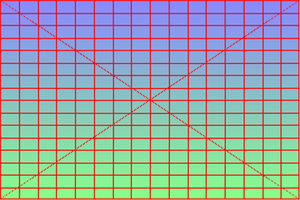
|
|
Distorting the expansion with sigmoidal. %IMDEV%convert ^ %SRC% ^ -gravity Center -extent 200%% ^ -define triangulate:sigmoidal=4,50%% ^ -distort Triangulate "%DISP_STR%" ^ -resize 50%% ^ tri_dimp1.png |

|
|
Distorting the expansion with power. %IMDEV%convert ^ %SRC% ^ -gravity Center -extent 200%% ^ -define triangulate:power=1.2 ^ -distort Triangulate "%DISP_STR%" ^ -resize 50%% ^ tri_dimp2.png |

|
These are similar to the IM operator -implode:
%IMDEV%convert ^ %SRC% ^ -implode 0.4 ^ tri_imp1.png |
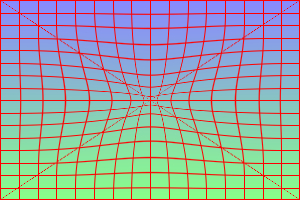
|
The effects are not identical. Compared to triangulate, the implode operator has a greater effect in the center and a lesser effect at the edge. The implode operator does not create discontinuitis of slope in the grid.
Make a zip file of differences to the normal IM source code, plus triangul.inc the new source code for triangulation, plus tritst.c the text-only test harness.
set IMCYGDEVDIR=/home/Alan/ImageMagick-6.9.0-0/ diff -u --strip-trailing-cr %IMCYGDEVDIR%factory/option.c ^ %IMCYGDEVDIR%magick/option.c >tri_option_c.diff diff -u --strip-trailing-cr %IMCYGDEVDIR%factory/distort.h ^ %IMCYGDEVDIR%magick/distort.h >tri_distort_h.diff diff -u --strip-trailing-cr %IMCYGDEVDIR%factory/distort.c ^ %IMCYGDEVDIR%magick/distort.c >tri_distort_c.diff del /y tri_src.zip zip tri_src.zip ^ tri_option_c.diff tri_distort_h.diff tri_distort_c.diff ^ %IMSRC%\magick\triangul.inc %IMSRC%\magick\tritst.c ^ %IMCYGDEVDIR%magick/triangul.h %IMCYGDEVDIR%magick/tritst.c
The zipfile tri_src.zip is available for download.
For convenience, .bat scripts are also available in a single zip file. See Zipped BAT files.
This is the source code that does all the work. It is a fragment of a program that needs to be included in a C or CPP program, such as distort.c (part of ImageMagick) or tritst.c given below.
// Rotation convention:
// Origin (0,0) is top-left.
// Edges around a vertex are linked in counter-clockwise order.
// Hence the three vertices of each triangle are visited in clockwise order.
typedef double CoordT;
typedef struct EdgeT EdgeT;
typedef struct TriangleT TriangleT;
typedef struct {
CoordT x, y;
EdgeT *firstEdge;
MagickBooleanType visited;
double * pArgs; /* Pointer to arguments for this point. */
} PointT;
typedef struct EdgeT {
PointT *org, *dst;
EdgeT *orgNext, *dstNext;
int numTri; /* 1 or 2. 1 means this is on convex hull. */
TriangleT * tri; /* A triangle that has this as an edge. */
} EdgeT;
typedef struct TriangleT {
PointT *p0, *p1, *p2;
double denominator;
CoordT centX, centY;
} TriangleT;
typedef enum {
oExtrapolate,
oClamp,
oBackground
} OutsideT;
typedef enum {
esShortest,
esLast
} EdgeSortT;
typedef struct {
/* Caller should populate these. */
MagickBooleanType verbose;
int NumPoints;
int NumArgsPp; /* Number of arguments per point, >=2. */
double * pArgs; /* Pointer to arguments for all points. */
int precision;
//MagickBooleanType background; // If true, don't bother calculating abc for pixels outside convex hull.
double ShiftCoords;
OutsideT outside;
double sigContrast, sigMidpoint;
double power;
MagickBooleanType CoordsLast; // If true, for each point, coordinates come after the data, not before.
EdgeSortT EdgeSort;
/* Internal use. */
int MaxNumPts;
int NumPts;
PointT * points;
int MaxNumEdges;
int NumEdges;
EdgeT * edges;
CoordT minX, minY, maxX, maxY;
int MaxNumTris;
int NumTris;
TriangleT * tris;
} SparseTriT;
typedef struct {
SparseTriT * st;
int PrevFndTri;
} SparseTriParaT;
typedef struct {
PointT *pa, *pb;
CoordT SqrDist;
int HiPntNum;
MagickBooleanType IsValid;
} CandidateEdgeT;
typedef enum {
iNoIntersect,
iSegment,
iEndPointAB,
iEndPointCD,
iMidPoint
} IntersectT;
#define perp(u,v) ((u).x * (v).y - (u).y * (v).x) // perp product (2D)
#define VectorT PointT
#define TRI_EPSILON 1e-7
static IntersectT SegsIntersect (PointT * A, PointT * B, PointT * C, PointT * D)
// Returns whether segments AB and CD intersect.
// Assumes A!=B and C!=D.
{
assert (A != B);
assert (C != D);
VectorT AB, CD, CA;
AB.x = B->x - A->x; //u
AB.y = B->y - A->y;
CD.x = D->x - C->x; //v
CD.y = D->y - C->y;
CA.x = A->x - C->x; //w
CA.y = A->y - C->y;
double Dp = perp(AB,CD);
if (fabs(Dp) < TRI_EPSILON) {
// They are parallel.
if (perp(AB,CA) != 0 || perp(CD,CA) != 0) return iNoIntersect;
// They are colinear.
double t0, t1;
VectorT CB;
CB.x = B->x - C->x;
CB.y = B->y - C->y;
if (CD.x != 0) {
t0 = CA.x / CD.x;
t1 = CB.x / CD.x;
} else {
t0 = CA.y / CD.y;
t1 = CB.y / CD.y;
}
if (t0 > t1) {
double t = t0;
t0 = t1;
t1 = t;
}
if (t0 > 1 || t1 < 0) return iNoIntersect;
t0 = (t0 < 0) ? 0 : t0;
t1 = (t1 > 1) ? 1 : t1;
//if (t0 == t1) {
if (t1-t0 < TRI_EPSILON) {
// They intersect at a point.
// *I0 = S2.P0 + t0 * v
if (t0 == 0 || t0 == 1) return iEndPointCD;
return iMidPoint;
}
// They intersect at a segment.
// *I0 = S2.P0 + t0 * v;
// *I1 = S2.P0 + t1 * v;
return iSegment;
}
// The segments are not parallel.
double sI = perp(CD,CA) / Dp;
if (sI < 0 || sI > 1) return iNoIntersect;
double tI = perp(AB,CA) / Dp;
if (tI < 0 || tI > 1) return iNoIntersect;
// *I0 = S1.P0 + sI * u;
if (sI == 0 || sI == 1) return iEndPointAB;
if (tI == 0 || tI == 1) return iEndPointCD;
return iMidPoint;
}
static MagickBooleanType IsHidden (PointT * A, PointT * B, PointT * C, PointT * D)
// Looking from A to B,
// returns whether B is hidden by edge from C to D.
// Merely sharing a common end-point does _not_ make one edge hidden by the other.
{
IntersectT it = SegsIntersect (A, B, C, D);
return (it == iSegment || it == iMidPoint);
}
static void UnitVect (PointT * A, PointT * B, PointT *C)
// Given vector AB, sets C so AC is the unit vector along AB.
// Assumes A and B are distinct. Otherwise, the unit vector is undefined.
{
CoordT dx = B->x - A->x;
CoordT dy = B->y - A->y;
CoordT len = sqrt (dx*dx + dy*dy);
assert (len != 0);
C->x = A->x + dx/len;
C->y = A->y + dy/len;
}
static inline CoordT PtsDistSqr (PointT * A, PointT * B)
// Returns squared distance between A and B.
{
CoordT dx = B->x - A->x;
CoordT dy = B->y - A->y;
return (dx*dx + dy*dy);
}
static inline CoordT PtsDist (PointT * A, PointT * B)
// Returns distance between A and B.
{
return sqrt (PtsDistSqr (A, B));
}
static inline CoordT AreaX2 (PointT * A, PointT * B, PointT * C)
{
return (- B->y * C->x
+ A->y * (-B->x + C->x)
+ A->x * (B->y - C->y)
+ B->x * C->y);
}
static double ProxDist (SparseTriT * st, PointT * A, PointT * B, PointT * C, MagickBooleanType sym)
/* Returns distance Au to Cu where B-Au and B-Cu are unit vectors in directions B-A and B-C.
Signed, for CW or CCW.
Distance Au to Cu is 2.0 if A is 180 degrees around B from C,
or zero if BA coincides with BC.
*/
{
PointT Au, Cu;
UnitVect (B, A, &Au); // Could optimize: this is repeated around each vertex.
UnitVect (B, C, &Cu);
CoordT len = PtsDist (&Au, &Cu);
if (len == 0) {
len = -TRI_EPSILON;
} else if (len >= 2) {
len = 2;
} else {
if (AreaX2 (A, B, C) > 0) len = -len;
}
return len;
}
static MagickBooleanType AddPoint (SparseTriT * st, CoordT x, CoordT y)
// Returns whether OK.
{
if (st->NumPts >= st->MaxNumPts) return MagickFalse;
PointT * pt = &st->points[st->NumPts];
if (st->ShiftCoords != 0) {
x += st->ShiftCoords * (drand48 () * 2 - 1);
y += st->ShiftCoords * (drand48 () * 2 - 1);
}
pt->x = x;
pt->y = y;
pt->firstEdge = NULL;
pt->visited = MagickFalse;
st->NumPts++;
if (st->NumPts == 1) {
st->minX = x;
st->minY = y;
st->maxX = x;
st->maxY = y;
} else {
if (st->minX > x) st->minX = x;
if (st->minY > y) st->minY = y;
if (st->maxX < x) st->maxX = x;
if (st->maxY < y) st->maxY = y;
}
return MagickTrue;
}
static inline EdgeT * NextEdge (EdgeT * e, PointT * p)
{
assert (p == e->org || p == e->dst);
return (p == e->org) ? e->orgNext : e->dstNext;
}
static inline PointT * OtherPoint (EdgeT * e, PointT * p)
{
assert (p == e->org || p == e->dst);
return (p == e->org) ? e->dst : e->org;
}
static EdgeT * FindEdgePosn (SparseTriT * st, PointT * p0, PointT * p1, MagickBooleanType sym)
// Finds position within ring of edges around p0 that is correct for new edge p0-p1.
// Returns prev, the edge in the ring after which this is to be inserted.
{
// Find three edges, not necessarily present or distinct.
EdgeT
*clsCCW = NULL, // edge CCW to p1 with shortest distance to p1
*clsCW = NULL, // edge CW to p1 with shortest distance to p1
*lastRight = NULL; // last CCW edge, before a CW edge
double distCCW = 9e9;
double distCW = -9e9;
MagickBooleanType FndCcw = MagickFalse;
MagickBooleanType FndFirstCw = MagickFalse;
EdgeT * prev = p0->firstEdge;
EdgeT * next = NextEdge (prev, p0);
EdgeT * first = next;
for (;;) {
assert (p0 == next->org || p0 == next->dst);
//printf (" fep %i ", OtherPoint (next, p0) - st->points);
double pd = ProxDist (st, p1, p0, OtherPoint (next, p0), sym);
if (pd > 0) {
// We have a CCW edge.
FndCcw = MagickTrue;
if (distCCW > pd) {
distCCW = pd;
clsCCW = next;
}
} else { // pd <= 0
// We have a CW edge.
if (FndCcw && !FndFirstCw) {
FndFirstCw = MagickTrue;
lastRight = prev;
}
if (distCW < pd) {
distCW = pd;
clsCW = prev;
//printf ("distCW=%g ", distCW);
}
}
prev = next;
next = NextEdge (next, p0);
if (next == first) {
// We sometimes need to go round twice.
if (!(!lastRight && clsCCW && clsCW)) {
break;
}
}
}
prev = NULL;
if (lastRight) prev = lastRight;
else if (clsCCW) prev = clsCCW;
else if (clsCW) prev = clsCW;
else fprintf (stderr, " FindEdgePosn: barf\n");
assert (prev);
//printf (" FindEdgePosn prev=%i\n", prev - st->edges);
return prev;
}
static MagickBooleanType AddEdge (SparseTriT * st, PointT * p0, PointT * p1)
// Returns whether OK.
{
assert (p0 != p1);
if (st->NumEdges >= st->MaxNumEdges) {
fprintf (stderr, "AddEdge bust\n");
return MagickFalse;
}
EdgeT * e = &st->edges[st->NumEdges];
//printf ("AddEdge %i points %i %i\n", st->NumEdges, p0 - st->points, p1 - st->points);
e->org = p0;
e->dst = p1;
e->orgNext = e->dstNext = e;
st->NumEdges++;
p0->visited = MagickTrue;
if (!p0->firstEdge) p0->firstEdge = e;
else {
//printf (" Nextp0 p0=%i firstEdge=%i ", p0 - st->points, p0->firstEdge - st->edges);
EdgeT * next = p0->firstEdge;
//EdgeT * prev = next;
EdgeT * prev = FindEdgePosn (st, p0, p1, p0==next->dst);
// Insert new edge after "prev".
//printf (" prev=%i New=%i\n", prev - st->edges, e - st->edges);
if (prev->org == p0) {
EdgeT * t = prev->orgNext;
prev->orgNext = e;
e->orgNext = t;
} else {
EdgeT * t = prev->dstNext;
prev->dstNext = e;
e->orgNext = t;
}
}
if (!p1->firstEdge) p1->firstEdge = e;
else {
//printf (" Nextp1 p1=%i firstEdge=%i ", p1 - st->points, p1->firstEdge - st->edges);
EdgeT * next = p1->firstEdge;
//EdgeT * prev = next;
EdgeT * prev = FindEdgePosn (st, p1, p0, p1==next->dst);
// Insert new edge after "prev".
//printf (" prev=%i New=%i\n", prev - st->edges, e - st->edges);
if (prev->org == p1) {
EdgeT * t = prev->orgNext;
prev->orgNext = e;
e->dstNext = t;
} else {
EdgeT * t = prev->dstNext;
prev->dstNext = e;
e->dstNext = t;
}
}
//WrVertexEdges (st, p0);
//WrVertexEdges (st, p1);
return MagickTrue;
}
static int comp_shortest (const void *a, const void *b)
// Sort by length, shortest first.
{
CoordT sda = ((const CandidateEdgeT *)a)->SqrDist;
CoordT sdb = ((const CandidateEdgeT *)b)->SqrDist;
// Sorting also by x and y isn't necessry,
// but helps when visually examining diagrams.
if (sda == sdb) {
sda = ((const CandidateEdgeT *)a)->pa->x;
sdb = ((const CandidateEdgeT *)b)->pb->x;
}
if (sda == sdb) {
sda = ((const CandidateEdgeT *)a)->pa->y;
sdb = ((const CandidateEdgeT *)b)->pb->y;
}
return (sda > sdb) - (sda < sdb);
}
static int comp_last (const void *a, const void *b)
// Sort by Highest Point Number, largest first.
{
int hpna = ((const CandidateEdgeT *)a)->HiPntNum;
int hpnb = ((const CandidateEdgeT *)b)->HiPntNum;
return (hpna < hpnb) - (hpna > hpnb);
}
static MagickBooleanType TriangulateSrtEdge (SparseTriT * st)
// Returns whether triangulation was possible.
{
printf ("TriangulateSrtEdge start\n");
// Build array of candidate edges.
//
int NumCand = st->NumPts * (st->NumPts-1) / 2;
if (NumCand <= 0) return MagickFalse;
CandidateEdgeT * ces = (CandidateEdgeT *)malloc (NumCand * sizeof (CandidateEdgeT));
if (!ces) {
fprintf (stderr, "oom ces");
exit (1);
}
printf ("TriangulateSrtEdge 1\n");
// Populate array of candidate edges.
//
int i, j;
CandidateEdgeT * ce = ces;
MagickBooleanType PointsCoincide = MagickFalse;
for (i = 0; i < st->NumPts-1; i++) {
PointT * pti = &st->points[i];
for (j = i+1; j < st->NumPts; j++) {
PointT * ptj = &st->points[j];
ce->pa = pti;
ce->pb = ptj;
ce->HiPntNum = j;
ce->IsValid = MagickTrue;
CoordT dx = ptj->x - pti->x;
CoordT dy = ptj->y - pti->y;
ce->SqrDist = dx*dx + dy*dy;
if (ce->SqrDist <= TRI_EPSILON) {
printf ("ce->SqrDist==0\n");
PointsCoincide = MagickTrue;
break;
}
ce++;
}
if (PointsCoincide == MagickTrue) break;
}
if (PointsCoincide == MagickTrue) return MagickFalse;
printf ("TriangulateSrtEdge 2\n");
// For every pair of candidate edges,
// if they intersect at a segment,
// declare the longer one as invalid.
ce = ces;
for (i = 0; i < NumCand-1; i++) {
if (ce->IsValid == MagickTrue) {
PointT * A = ce->pa;
PointT * B = ce->pb;
CandidateEdgeT * ceB = ce + 1;
for (j = i+1; j < NumCand; j++) {
if (ceB->IsValid == MagickTrue) {
PointT * C = ceB->pa;
PointT * D = ceB->pb;
if (SegsIntersect (A, B, C, D) == iSegment) {
printf ("TriangulateSrtEdge %i and %i intersect at segment\n", i, j);
if (ce->SqrDist > ceB->SqrDist) {
ce->IsValid = MagickFalse;
} else {
ceB->IsValid = MagickFalse;
}
}
}
ceB++;
}
}
ce++;
}
printf ("TriangulateSrtEdge 3\n");
// Sort array of candidate edges.
//
switch (st->EdgeSort) {
default:
case esShortest:
qsort ((void *)ces, NumCand, sizeof (CandidateEdgeT), comp_shortest);
break;
case esLast:
qsort ((void *)ces, NumCand, sizeof (CandidateEdgeT), comp_last);
break;
}
printf ("TriangulateSrtEdge 4\n");
// For each candidate edge, are the ends hidden by an existing edge?
// If not, then add candidate edge as an actual edge.
//
int n, ie;
ce = ces;
for (n = 0; n < NumCand; n++) {
if (ce->IsValid) {
MagickBooleanType hidden = MagickFalse;
for (ie = 0; ie < st->NumEdges; ie++) {
EdgeT * e = &st->edges[ie];
hidden = IsHidden (ce->pa, ce->pb, e->org, e->dst);
if (hidden) break;
}
if (!hidden) {
if (!AddEdge (st, ce->pa, ce->pb)) return MagickFalse;
}
}
ce++;
}
free (ces);
printf ("TriangulateSrtEdge end\n");
return MagickTrue;
}
static MagickBooleanType AddTriangles (SparseTriT * st)
// Find the triangles.
// Each triangle has vertices listed in clockwise order.
// (Strictly speaking, each face is listed with vertices in the order such that the face
// is on the right of each edge. The algorithm would also find the convex hull,
// where the face is outside all the points.)
// This would give three listings per triangle,
// so we choose the one with lowest first vertex.
{
printf ("Triangles:\n");
printf ("T=%i\n", st->NumEdges - st->NumPts + 2);
if (st->NumPts < 3) return MagickFalse;
int i;
for (i = 0; i < st->NumEdges; i++) {
EdgeT * e = &st->edges[i];
e->tri = NULL;
e->numTri = 0;
}
st->MaxNumTris = st->NumEdges - st->NumPts + 4;
st->NumTris = 0;
st->tris = (TriangleT *) malloc (st->MaxNumTris * sizeof (TriangleT));
if (!st->tris) {
fprintf (stderr, "oom tris");
return MagickFalse;
}
int CntTri = 0;
for (i = 0; i < st->NumPts; i++) {
PointT * p0 = &st->points[i];
EdgeT * e0 = p0->firstEdge;
do {
PointT * p1 = OtherPoint (e0, p0);
//printf ("\np0,p1: %i %i ", p0 - st->points, p1 - st->points);
if (p0 < p1) {
EdgeT * e1 = NextEdge (e0, p1);
PointT * p2 = OtherPoint (e1, p1);
EdgeT * e2 = NextEdge (e1, p2);
PointT * p3 = OtherPoint (e2, p2);
if (p0 < p2) {
if (p3 == p0 && AreaX2 (p0, p1, p2) > 0) {
printf (" triPts: %li %li %li # %i\n",
(long int)(p0 - st->points),
(long int)(p1 - st->points),
(long int)(p2 - st->points), CntTri);
printf (" tri: %g %g %g %g %g %g",
p0->x, p0->y, p1->x, p1->y, p2->x, p2->y);
printf (" A=%.*g\n", st->precision, AreaX2 (p0, p1, p2)/2);
if (st->NumTris >= st->MaxNumTris) {
fprintf (stderr, "AddTriangles bust\n");
return MagickFalse;
}
TriangleT * ptri = &st->tris[st->NumTris];
ptri->p0 = p0;
ptri->p1 = p1;
ptri->p2 = p2;
ptri->denominator =
(p1->y - p2->y)*(p0->x - p2->x)
+ (p2->x - p1->x)*(p0->y - p2->y);
assert (ptri->denominator != 0);
ptri->centX = (p0->x + p1->x + p2->x) / 3;
ptri->centY = (p0->y + p1->y + p2->y) / 3;
e0->tri = ptri;
e1->tri = ptri;
e2->tri = ptri;
e0->numTri++;
e1->numTri++;
e2->numTri++;
st->NumTris++;
CntTri++;
} else {
printf ("AddTriangles p0!=p3 or neg area ");
printf (" dt pts %li %li %li %li",
(long int)(p0 - st->points),
(long int)(p1 - st->points),
(long int)(p2 - st->points),
(long int)(p3 - st->points));
if (p3 == p0) {
printf (" AreaX2=%g", AreaX2 (p0, p1, p2));
}
printf ("\n");
}
}
}
e0 = NextEdge (e0, p0);
} while (e0 != p0->firstEdge);
}
printf ("CntTri: %i\n", CntTri);
if (st->NumTris) {
printf ("Integrity check of st: %i edges: \n", st->NumEdges);
for (i = 0; i < st->NumEdges; i++) {
EdgeT * e = &st->edges[i];
printf ("%i %i", i, e->numTri);
if (e->numTri == 0) printf (" *****");
else assert (e->tri != NULL);
printf ("\n");
}
printf ("\n");
}
return MagickTrue;
}
static void DumpPoints (SparseTriT * st, FILE * fh)
{
fprintf (fh, "NumPoints: %i\n", st->NumPts);
int i;
int CntEdge = 0;
for (i = 0; i < st->NumPts; i++) {
PointT * pt = &st->points[i];
fprintf (fh, " point: %.*g %.*g # %i\n",
st->precision, pt->x, st->precision, pt->y, i);
if (pt->firstEdge) {
EdgeT * e = pt->firstEdge;
fprintf (fh, " first: %li pts: %li %li\n",
(long int)(e - st->edges),
(long int)(e->org - st->points),
(long int)(e->dst - st->points));
CntEdge++;
int Limit = 20;
do {
e = NextEdge (e, pt);
if (e == pt->firstEdge) break;
fprintf (fh, " next: %li pts: %li %li\n",
(long int)(e - st->edges),
(long int)(e->org - st->points),
(long int)(e->dst - st->points));
CntEdge++;
Limit--;
} while (e != pt->firstEdge && Limit > 0);
if (Limit == 0) fprintf (fh, "Loop?\n");
}
}
fprintf (fh, "CountedEdges: %i\n", CntEdge);
}
static void DumpEdges (SparseTriT * st, FILE * fh)
{
fprintf (fh, "NumEdges: %i\n", st->NumEdges);
int i;
for (i = 0; i < st->NumEdges; i++) {
EdgeT * e = &st->edges[i];
fprintf (fh, " edge: %.*g %.*g %.*g %.*g pts: %li %li # %i numTri: %i",
st->precision, e->org->x, st->precision, e->org->y,
st->precision, e->dst->x, st->precision, e->dst->y,
(long int)(st->points - e->org),
(long int)(st->points - e->dst),
i,
e->numTri);
if (e->numTri) {
fprintf (fh, " tri: %li",
(long int)(e->tri - st->tris));
} else {
fprintf (fh, " tri: null");
}
fprintf (fh, "\n");
}
}
static void DumpTriangles (SparseTriT * st, FILE * fh)
{
fprintf (fh, "NumTriangles: %i\n", st->NumTris);
int i;
for (i = 0; i < st->NumTris; i++) {
TriangleT * tri = &st->tris[i];
fprintf (fh, " trianglePts: %li %li %li # %i\n",
(long int)(tri->p0 - st->points),
(long int)(tri->p1 - st->points),
(long int)(tri->p2 - st->points),
i);
fprintf (fh, " triangle: %.*g %.*g %.*g %.*g %.*g %.*g\n",
st->precision, tri->p0->x, st->precision, tri->p0->y,
st->precision, tri->p1->x, st->precision, tri->p1->y,
st->precision, tri->p2->x, st->precision, tri->p2->y);
fprintf (fh, " triangleCentXY: %.*g %.*g\n",
st->precision, tri->centX, st->precision, tri->centY);
}
}
static void DeInitTri (SparseTriT * st)
{
if (st->MaxNumPts) free (st->points);
if (st->MaxNumEdges) free (st->edges);
st->NumPoints = 0;
st->MaxNumPts = 0;
st->NumPts = 0;
st->MaxNumEdges = 0;
st->NumEdges = 0;
if (st->MaxNumTris > 0) free (st->tris);
st->MaxNumTris = 0;
st->NumTris = 0;
}
static MagickBooleanType InitTri (SparseTriT * st)
/* Args is address of first element of an array with (NumPoints*NumArgsPerPnt) values.
Within each group of NumArgsPerPnt values, first two are x,y coords.
Others are values for the barycentric weighting.
Returns whether OK. If false, no need to call DeInitTri.
*/
{
if (st->NumPoints < 1) return MagickFalse;
if (st->NumArgsPp < 2) return MagickFalse;
st->MaxNumPts = st->NumPoints;
st->NumPts = 0;
st->points = (PointT *) malloc (st->MaxNumPts * sizeof (PointT));
if (!st->points) {
st->MaxNumPts = 0;
return MagickFalse;
}
st->MaxNumEdges = st->NumPoints * 3;
st->NumEdges = 0;
st->edges = (EdgeT *) malloc (st->MaxNumEdges * sizeof (EdgeT));
if (!st->edges) {
DeInitTri (st);
return MagickFalse;
};
st->MaxNumTris = 0;
st->NumTris = 0;
st->tris = NULL;
int CoordOffset = st->CoordsLast ? st->NumArgsPp-2 : 0;
int DataOffset = st->CoordsLast ? 0 : 2;
CoordOffset = 0;
DataOffset = 2;
int i;
for (i = 0; i < st->NumPoints; i++) {
if (!AddPoint (st,
st->pArgs[i*st->NumArgsPp+CoordOffset],
st->pArgs[i*st->NumArgsPp+CoordOffset+1]))
{
DeInitTri (st);
return MagickFalse;
}
if (st->NumArgsPp <=2)
st->points[i].pArgs = NULL;
else
st->points[i].pArgs = &st->pArgs[i*st->NumArgsPp+DataOffset];
}
if (!TriangulateSrtEdge (st)) {
DeInitTri (st);
return MagickFalse;
}
AddTriangles (st);
if (st->verbose) {
fprintf (stderr, "MinCoord: %.*g %.*g\n",
st->precision, st->minX, st->precision, st->minY);
fprintf (stderr, "MaxCoord: %.*g %.*g\n",
st->precision, st->maxX, st->precision, st->maxY);
DumpPoints (st, stderr);
DumpEdges (st, stderr);
DumpTriangles (st, stderr);
}
return MagickTrue;
}
/* ---------------------------------------------------------------
End of triangulation functions.
Next function: find the triangle for a point.
-----------------------------------------------------------------*/
static CoordT inline DistanceZeroOne (CoordT a)
{
return (a < 0) ? -a : ( (a >= 1) ? a-1 : 0 );
}
static CoordT inline DistanceZero (CoordT a)
{
return (a < 0) ? -a : 0;
}
static MagickBooleanType inline WithinZeroOne (CoordT a)
{
return (DistanceZeroOne(a) < TRI_EPSILON);
}
static void inline Clamp01 (double * a)
{
*a = (*a <= 0) ? 0 : ( (*a >= 1) ? 1 : *a );
}
/*---
static double PerpDist (SparseTriT * st, PointT * A, PointT * B, PointT * C)
// Retuns perpendicular distance from A to infinite line defined by B and C.
// Assumes B and C are distinct.
{
double dx = C->x - B->x;
double dy = C->y - B->y;
double lenSqr = dx*dx + dy*dy;
assert (lenSqr != 0);
double area = fabs(AreaX2 (A, B, C))/2;
return area / sqrt(lenSqr);
}
---*/
static double ShortestDist (SparseTriT * st, PointT * A, PointT * B, PointT * C, int Debug)
// Finds shortest distance between A and segment BC.
// This is either distance AB or distance BC
// or (where perp dropped from A to line BC is within BC) the perp distance.
{
// Where AB is line and C is point:
//t=[(Cx-Ax)(Bx-Ax)+(Cy-Ay)(By-Ay)]/[(Bx-Ax)^2+(By-Ay)^2]
// Where BC is line and A is point:
// FIXME: efficiency: pre-calculate edge squared lengths.
double dx = C->x - B->x;
double dy = C->y - B->y;
//if (Debug) printf ("dx=%g dy=%g numer=%g denom=%g ",
// dx, dy, ((A->x - B->x)*dx + (A->y - B->y)*dy), (dx*dx+dy*dy));
double t = ((A->x - B->x)*dx + (A->y - B->y)*dy)
/ (dx*dx + dy*dy);
// t is parametric distance along infinite line defined by BC of perpendicular dropped from A.
// eg if dx==0, t = (A->y - B->y)/dy
//N->x=Ax+t(Bx-Ax)
//N->y=Ay+t(By-Ay)
if (Debug) printf ("t=%g ", t);
Clamp01 (&t);
double fndX = B->x + t * (C->x-B->x);
double fndY = B->y + t * (C->y-B->y);
if (Debug) {
printf ("fndXY %g %g ", fndX, fndY);
}
dx = fndX - A->x;
dy = fndY - A->y;
return sqrt (dx*dx + dy*dy); // FIXME: efficiency: we don't need to sqrt it.
}
static void inline CalcAbc (SparseTriT * st, CoordT x, CoordT y,
TriangleT * t,
CoordT * a, CoordT * b, CoordT * c, MagickBooleanType Normalise)
{
Normalise = MagickTrue;
*a = ((t->p1->y - t->p2->y)*(x - t->p2->x) + (t->p2->x - t->p1->x)*(y - t->p2->y))
/ t->denominator;
*b = ((t->p2->y - t->p0->y)*(x - t->p2->x) + (t->p0->x - t->p2->x)*(y - t->p2->y))
/ t->denominator;
*c = 1 - *a - *b;
if (!Normalise) {
*a *= t->denominator;
*b *= t->denominator;
*c *= t->denominator;
}
}
static CoordT inline WorstAbc (SparseTriT * st, CoordT x, CoordT y,
TriangleT * t)
{
CoordT a, b, c;
CalcAbc (st, x, y, t, &a, &b, &c, MagickFalse);
// For non-normalised, just test against zero.
a = DistanceZeroOne (a);
b = DistanceZeroOne (b);
c = DistanceZeroOne (c);
if (b > a) a = b;
if (c > a) a = c;
return a;
}
static CoordT inline CosAng (PointT * A, PointT * B, PointT * C)
// Returns cosine of angle BAC.
// CosBAC = (b^2 + c^2 - a^2) / (2.b.c)
{
CoordT a2 = PtsDistSqr (B, C);
CoordT b2 = PtsDistSqr (C, A);
CoordT c2 = PtsDistSqr (A, B);
return (b2 + c2 - a2) / (2 * sqrt(b2) * sqrt(c2));
}
//#define DEBUG_COND (x < 10 && y < 10)
//#define DEBUG_COND ((x > 170 && x < 180 && y > 190) || (x > 188 && x < 202 && y > 196 && y < 201))
//#define DEBUG_COND (x > 188 && x < 202 && y > 43 && y < 52)
//#define DEBUG_COND (x > 130 && x < 135 && y > 190)
//#define DEBUG_COND (x > 138 && x < 146 && y > 90 && y < 97)
//#define DEBUG_COND (x > 130 && x < 150 && y > 80 && y < 100)
#define DEBUG_COND (1==0)
static EdgeT * NearestEdge (SparseTriT * st, CoordT x, CoordT y)
// Finds nearest edge on the convex hull.
{
PointT A;
A.x = x;
A.y = y;
int i;
double v;
double leastV = 9e9;
EdgeT * fndE1 = NULL;
EdgeT * fndE2 = NULL;
for (i = 0; i < st->NumEdges; i++) {
EdgeT * e = &st->edges[i];
if (e->numTri == 1) {
v = ShortestDist (st, &A, e->org, e->dst, DEBUG_COND);
if (DEBUG_COND) {
printf ("Edge=%i v=%g\n", i, v);
}
if (leastV > v) {
leastV = v;
fndE1 = e;
}
}
}
assert (fndE1);
if (DEBUG_COND) {
printf ("fndE=%li \n", (long int)(fndE1 - st->edges));
}
// Do we have another edge at practically the same distance?
for (i = 0; i < st->NumEdges; i++) {
EdgeT * e = &st->edges[i];
if (e->numTri == 1 && e != fndE1) {
v = ShortestDist (st, &A, e->org, e->dst, DEBUG_COND);
if (fabs (leastV - v) < TRI_EPSILON) {
fndE2 = e;
}
}
}
// If two edges are equal, they probably have a common point which we are close to.
// Choose the edge that gives the largest angle (e->p0, {x,y}, e->p1).
if (fndE2) {
CoordT cos1 = CosAng (&A, fndE1->org, fndE1->dst);
CoordT cos2 = CosAng (&A, fndE2->org, fndE2->dst);
if (DEBUG_COND) {
printf ("fndE2=%li cos=%g %g \n",
(long int)(fndE2 - st->edges),
cos1, cos2);
}
if (cos2 < cos1) fndE1 = fndE2;
}
return fndE1;
}
static MagickBooleanType FindTriangle
(SparseTriParaT * stp, CoordT x, CoordT y,
TriangleT ** tri,
CoordT * a, CoordT * b, CoordT * c)
/* Returns whether this coord is within convex hull of triangulated points. */
/* If there are no triangles, don't call this. */
{
// FIXME: probably worth checking for st->NumTris==1.
int i;
MagickBooleanType FoundExact = MagickFalse;
for (i = 0; i < stp->st->NumTris; i++) {
int TriNum = (i+stp->PrevFndTri) % stp->st->NumTris;
TriangleT * t = &stp->st->tris[TriNum];
*tri = t;
CalcAbc (stp->st, x, y, t, a, b, c, MagickTrue);
if (DEBUG_COND) {
printf ("xy=%g %g PrevTri=%i Tri=%i abc=%g %g %g \n",
x, y, stp->PrevFndTri, TriNum, *a, *b, *c);
}
if (WithinZeroOne (*a) && WithinZeroOne (*b) && WithinZeroOne (*c)) {
stp->PrevFndTri = TriNum;
FoundExact = MagickTrue;
break;
}
/*---
CoordT d = DistanceZeroOne (*a);
if (d > 0 && d < SmallestN01Dist) {
SmallestN01Dist = d;
ClosestTri = TriNum;
}
d = DistanceZeroOne (*b);
if (d > 0 && d < SmallestN01Dist) {
SmallestN01Dist = d;
ClosestTri = TriNum;
}
d = DistanceZeroOne (*c);
if (d > 0 && d < SmallestN01Dist) {
SmallestN01Dist = d;
ClosestTri = TriNum;
}
---*/
}
if (!FoundExact && stp->st->outside != oBackground) {
EdgeT * e = NearestEdge (stp->st, x, y);
*tri = e->tri;
#if 0
// Find the least worst triangle.
CoordT LeastV = 99e9;
for (i = 0; i < st->NumTris; i++) {
int TriNum = (i+st->PrevFndTri) % st->NumTris;
TriangleT * t = &st->tris[TriNum];
CoordT v = WorstAbc (st, x, y, t);
if (LeastV > v) {
LeastV = v;
st->PrevFndTri = TriNum;
*tri = t;
}
if (DEBUG_COND) {
printf ("Tri %i Worst=%g, LeastV=%g \n", TriNum, v, LeastV);
}
/*---
double dx = x - t->centX;
double dy = y - t->centY;
double distSq = dx*dx + dy*dy;
if (DEBUG_COND) {
printf ("DistSq=%g \n", distSq);
}
if (LeastV > distSq) {
LeastV = distSq;
st->PrevFndTri = TriNum;
*tri = t;
}
---*/
}
if (DEBUG_COND) {
printf ("LeastV=%g ClosestTri=%li \n", LeastV, (long int)(*tri - st->tris));
}
#endif
if (DEBUG_COND) {
printf ("ClosestTri=%li \n", (long int)(*tri - stp->st->tris));
}
CalcAbc (stp->st, x, y, *tri, a, b, c, MagickFalse);
}
return FoundExact;
}
/* ---------------------------------------------------------------
Sigmoidal processing, copied from enhance.c
a is contrast
b is midpoint, 0.0 <= b <= 1.0
x is the value to be converted, 0.0 <= x <= 1.0.
--------------------------------------------------------------- */
#if defined(MAGICKCORE_HAVE_ATANH)
#define Sigmoidal(a,b,x) ( tanh((0.5*(a))*((x)-(b))) )
#else
#define Sigmoidal(a,b,x) ( 1.0/(1.0+exp((a)*((b)-(x)))) )
#endif
#define ScaledSigmoidal(a,b,x) ( \
(Sigmoidal((a),(b),(x))-Sigmoidal((a),(b),0.0)) / \
(Sigmoidal((a),(b),1.0)-Sigmoidal((a),(b),0.0)) )
static inline double InverseScaledSigmoidal(const double a,const double b,
const double x)
{
const double sig0=Sigmoidal(a,b,0.0);
const double sig1=Sigmoidal(a,b,1.0);
const double argument=(sig1-sig0)*x+sig0;
const double clamped=
(
#if defined(MAGICKCORE_HAVE_ATANH)
argument < -1+MagickEpsilon
?
-1+MagickEpsilon
:
( argument > 1-MagickEpsilon ? 1-MagickEpsilon : argument )
);
return(b+(2.0/a)*atanh(clamped));
#else
argument < MagickEpsilon
?
MagickEpsilon
:
( argument > 1-MagickEpsilon ? 1-MagickEpsilon : argument )
);
return(b-log(1.0/clamped-1.0)/a);
#endif
}
/* ---------------------------------------------------------------
Entry points:
--------------------------------------------------------------- */
static inline double AbcPow (double abc, double p)
{
return (abc < 0) ? -pow(-abc,p) : pow(abc,p);
}
static MagickBooleanType GetTriVals
(SparseTriParaT * stp, CoordT x, CoordT y, double ** TriRetVals)
/* TriRetVals must be an array already allocated (and eventally freed)
by the caller with at least (NumArgsPp-2) entries. */
{
if (!stp->st->NumTris) return MagickFalse;
CoordT a, b, c;
TriangleT * tri = NULL;
if (DEBUG_COND) {
printf ("xy=%g %g ", x, y);
}
MagickBooleanType FndExact = FindTriangle (stp, x, y, &tri, &a, &b, &c);
if (FndExact || stp->st->outside != oBackground) {
if (DEBUG_COND) {
printf ("Exact=%i tri=%li abc=%g %g %g ",
FndExact, (long int)(tri - stp->st->tris), a, b, c);
}
if (stp->st->power != 1.0) {
a = AbcPow (a, stp->st->power);
b = AbcPow (b, stp->st->power);
c = AbcPow (c, stp->st->power);
}
if (stp->st->sigContrast > 0.0) {
a = ScaledSigmoidal(stp->st->sigContrast,stp->st->sigMidpoint,a);
b = ScaledSigmoidal(stp->st->sigContrast,stp->st->sigMidpoint,b);
c = ScaledSigmoidal(stp->st->sigContrast,stp->st->sigMidpoint,c);
} else if (stp->st->sigContrast < 0.0) {
a = InverseScaledSigmoidal(-stp->st->sigContrast,stp->st->sigMidpoint,a);
b = InverseScaledSigmoidal(-stp->st->sigContrast,stp->st->sigMidpoint,b);
c = InverseScaledSigmoidal(-stp->st->sigContrast,stp->st->sigMidpoint,c);
}
if (stp->st->outside == oClamp) {
Clamp01 (&a);
Clamp01 (&b);
Clamp01 (&c);
}
double div = a + b + c;
int i;
for (i = 0; i < stp->st->NumArgsPp-2; i++) {
(*TriRetVals)[i] = (tri->p0->pArgs[i] * a
+ tri->p1->pArgs[i] * b
+ tri->p2->pArgs[i] * c) / div;
if (DEBUG_COND) {
printf ("RV[%i]=%g ", i, (*TriRetVals)[i]);
}
}
if (DEBUG_COND) {
printf ("\n");
}
}
return FndExact;
}
void TriDefaultValues (SparseTriT * st)
{
st->verbose = MagickFalse;
st->NumPoints = 0;
st->NumArgsPp = 2;
st->pArgs = NULL;
st->precision = 6;
st->ShiftCoords = 0.0;
st->outside = oExtrapolate;
st->sigContrast = 0.0;
st->sigMidpoint = 0.5;
st->power = 1.0;
st->CoordsLast = MagickFalse;
st->EdgeSort = esShortest;
st->MaxNumPts = 0;
st->NumPts = 0;
st->points = NULL;
st->MaxNumEdges = 0;
st->NumEdges = 0;
st->edges = NULL;
st->minX = st->minY = st->maxX = st->maxY = 0;
st->MaxNumTris = 0;
st->NumTris = 0;
st->tris = NULL;
}
This is a shell program for testing triangul.inc given above. It does not need to be linked to any ImageMagick software. It can be compiled with:
gcc -Wall -o tritst.exe tritst.c
The program reads points from stdin, and triangulates them, writing text results.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <assert.h>
#define MagickBooleanType int
#define MagickTrue 1
#define MagickFalse 0
#define MagickEpsilon 1e-10
#include "triangul.inc"
static void TestShortestDist (SparseTriT * st, PointT * A, PointT * B, PointT * C)
{
printf ("BC=(%g %g)(%g %g) ", B->x, B->y, C->x, C->y);
printf ("xy=%g %g ", A->x, A->y);
double r = ShortestDist (st, A, B, C, MagickTrue);
printf ("r=%g\n", r);
}
static void TSD (void)
{
printf ("\n\nTSD\n");
SparseTriT st;
PointT A, B, C;
B.x = 90;
B.y = 110;
C.x = 110;
C.y = 90;
A.x = 91;
A.y = 91;
TestShortestDist (&st, &A, &B, &C);
A.x = 91;
A.y = 111;
TestShortestDist (&st, &A, &B, &C);
A.x = 91;
A.y = 109;
TestShortestDist (&st, &A, &B, &C);
int i;
for (i=0; i <= 22; i++) {
A.x = 90+i;
A.y = 110-i;
TestShortestDist (&st, &A, &B, &C);
}
A.x = 101;
A.y = 101;
TestShortestDist (&st, &A, &B, &C);
B.x = 90;
B.y = 110;
C.x = 90;
C.y = 130;
printf ("110 to 130\n");
for (i=0; i <= 22; i++) {
A.x = 93;
A.y = 110+i;
TestShortestDist (&st, &A, &B, &C);
}
for (i=0; i <= 22; i++) {
A.x = 87;
A.y = 110+i;
TestShortestDist (&st, &A, &B, &C);
}
}
int main (void)
{
SparseTriT st;
double * TriRetVals;
TriDefaultValues (&st);
st.verbose = MagickTrue;
st.precision = 9;
if (scanf("%d %d", &st.NumPoints, &st.NumArgsPp) != 2) {
fprintf (stderr, "Problem reading first line\n");
return 0;
}
if (st.NumPoints <= 0) {
fprintf (stderr, "Number of points has to be greater than 0\n");
return 0;
}
if (st.NumArgsPp < 2) {
fprintf (stderr, "Number of arguments per point has to be at least 2\n");
return 0;
}
printf ("Reading %i points each with %i arguments.\n", st.NumPoints, st.NumArgsPp);
st.pArgs = (double *) malloc(st.NumPoints * st.NumArgsPp * sizeof (double));
if (!st.pArgs) {
printf ("oom st.pArgs");
exit (1);
}
if (st.NumArgsPp > 2) {
TriRetVals = (double *) malloc((st.NumArgsPp-2) * sizeof (double));
if (!TriRetVals) {
printf ("oom TriRetVals");
exit (1);
}
}
int i;
for (i = 0; i < st.NumPoints*st.NumArgsPp; i++) {
if (scanf("%lg", &st.pArgs[i]) != 1) {
fprintf (stderr, "Problem reading data item %i\n", i);
return 0;
}
//printf ("%g ", st.pArgs[i]);
}
printf ("Call InitTri\n");
if (InitTri (&st) == MagickFalse) {
printf ("InitTri failed");
exit (1);
}
printf ("Finished InitTri\n");
SparseTriParaT stp;
stp.st = &st;
stp.PrevFndTri = 0;
// Exercise GetTriVals.
int x, y;
st.maxX = 300;
st.maxY = 200;
for (y = 0; y < st.maxY; y++) {
for (x = 0; x < st.maxX; x++) {
GetTriVals (&stp, x, y, &TriRetVals);
if (stp.st->NumArgsPp > 2 && x < 10 && y < 10 ) {
printf ("%i %i RV:", x, y);
for (i = 0; i < stp.st->NumArgsPp-2; i++) printf (" %g", TriRetVals[i]);
printf ("\n");
}
}
}
DeInitTri (&st);
if (st.NumArgsPp > 2) {
free (TriRetVals);
}
free (st.pArgs);
//TSD ();
return 0;
}
This runs tritst.exe, and creates two image files and various text files.
The script calls convTriImg.bat which uses utility programs such as cGrep.exe, chStrs.exe and cPrefix.exe. I do not provide source or binaries of these.
rem Given %1 is points data file, rem makes %2_out.lis and image files. @if "%2"=="" findstr /B "rem @rem" %~f0 & exit /B 1 @setlocal rem @call echoOffSave set INFILE=%1 if "%INFILE%"=="" set INFILE=data.dat set OUTBASE=%2 if "%OUTBASE%"=="" set OUTBASE=data set OUTLIS=%OUTBASE%_out.lis del /s %OUTLIS% 2>nul tritst <%INFILE% 2>%OUTLIS% if ERRORLEVEL 1 ( echo %0: tritst failed goto end ) call %PICTBAT%convTriImg %OUTLIS% %OUTBASE% :end call echoRestore @endlocal
This uses utility programs cGrep.exe, chStrs.exe and cPrefix.exe. I don't provide the source or binaries of these.
rem From %1, the text output from "-verbose" triangulate,
rem makes %2_l.png, %2_t.png and %2_c.png
rem showing lines, triangles and convex hull.
@if "%2"=="" findstr /B "rem @rem" %~f0 & exit /B 1
@setlocal
rem @call echoOffSave
set INLIS=%1
set OUTBASE=%2
if "%OUTBASE%"=="" set OUTBASE=data
set OUTLINES=%OUTBASE%_l.png
set OUTEDGES=%OUTBASE%_e.png
set OUTTRI=%OUTBASE%_t.png
set OUTCONV=%OUTBASE%_c.png
rem type %INLIS%
set WW=
for /F "tokens=2,3 usebackq delims=:, " %%A in (`cGrep /p0 /i%INLIS% /sMaxCoord:*`) do (
rem set /A WW=1+%%A
rem set /A HH=1+%%B
for /F "usebackq" %%L in (`%IM%identify ^
-ping ^
-format "WW=%%[fx:int(%%A+20)]\nHH=%%[fx:int(%%B+20)]" ^
xc:`) do set %%L
)
if "%WW%"=="" (
echo %0: WW not set. Not "-verbose" output? stderr not captured?
exit /B 1
)
echo WW=%WW% HH=%HH%
set /A PNTSIZE=%WW%/60
if %PNTSIZE% LSS 20 set PNTSIZE=20
set /A H_MARG=%PNTSIZE%*3/2
set /A V_MARG=%PNTSIZE%*3/4
set /A Wm=%WW%-%H_MARG%
set /A Hm=%HH%-%V_MARG%
cGrep /i%INLIS% /opoints.txt /s"point:"
:: points2.txt isn't used
(for /F "tokens=2,3 usebackq delims=:, " %%A in (`cGrep /p0 /i%INLIS% /s*point:*`) do @(
@rem @set /A newY=50+%%B
@for /F "usebackq" %%L in (`%IM%identify ^
-ping ^
-format "newY=%%[fx:%%B+50]" ^
xc:`) do @set %%L
@echo circle %%A,%%B,%%A,!newY!
)) >points2.txt
(for /F "tokens=2-4 usebackq delims=:,# " %%A in (`cGrep /p0 /i%INLIS% /s*point:*`) do @(
@rem @set /A x=%%A
@rem @set /A y=%%B
@for /F "usebackq" %%L in (`%IM%identify ^
-ping ^
-format "x=%%[fx:int(%%A)]\ny=%%[fx:int(%%B)]" ^
xc:`) do @set %%L
@if !x! GTR %Wm% set /A x=!x!-%H_MARG%
@if !y! LSS %V_MARG% set /A y=%V_MARG%
@echo text !x!,!y! "%%C"
)) >pointsNum.txt
(for /F "tokens=2-6 usebackq delims=:,# " %%A in (`cGrep /p0 /i%INLIS% /s*edge:*`) do @(
@rem @set /A x=^(%%A+%%C^)/2
@rem @set /A y=^(%%B+%%D^)/2
@rem @set /A x=%%A/2+%%C/2
@rem @set /A y=%%B/2+%%D/2
@for /F "usebackq" %%L in (`%IM%identify ^
-ping ^
-format "x=%%[fx:int((%%A+%%C)/2)]\ny=%%[fx:int((%%B+%%D)/2)]" ^
xc:`) do @set %%L
@if !x! GTR %Wm% set /A x=!x!-%H_MARG%
@if !y! LSS %V_MARG% set /A y=%V_MARG%
@echo text !x!,!y! "%%E"
)) >edgeNum.txt
(for /F "tokens=2-7 usebackq delims=:,# " %%A in (`cGrep /p0 /i%INLIS% /s*triangle:*`) do @(
@echo polygon %%A,%%B %%C,%%D %%E,%%F
)) >tri.txt
set count=0
(for /F "tokens=2-7 usebackq delims=:,# " %%A in (`cGrep /p0 /i%INLIS% /s*triangle:*`) do @(
@rem @set /A x=^(%%A+%%C+%%E^)/3
@rem @set /A y=^(%%B+%%D+%%F^)/3
@rem @set /A x=%%A/3+%%C/3+%%E/3
@rem @set /A y=%%B/3+%%D/3+%%F/3
@for /F "usebackq" %%L in (`%IM%identify ^
-ping ^
-format "x=%%[fx:int((%%A+%%C+%%E)/3)]\ny=%%[fx:int((%%B+%%D+%%F)/3)]" ^
xc:`) do @set %%L
@if !x! GTR %Wm% set /A x=!x!-%H_MARG%
@if !y! LSS %V_MARG% set /A y=%V_MARG%
@echo text !x!,!y! "!count!"
@set /A count+=1
)) >triNum.txt
chStrs /p0 /ipoints.txt /f" point: " /t"\0"
chStrs /p0 /ipoints.txt /f" " /t","
cPrefix /p0 /ipoints.txt /l"translate " /r" circle 0,0 0,20"
rem type points.txt
rem type points2.txt
cGrep /p0 /i%INLIS% /olines.txt /s"edge:"
chStrs /p0 /ilines.txt /f"edge:" /t"line"
%IM%convert ^
-size %WW%x%HH% xc:None ^
-stroke #000 -fill None ^
-draw "@lines.txt" ^
-pointsize %PNTSIZE% -fill #a00 -stroke None ^
-undercolor rgba(100%%,100%%,100%%,0.5) ^
-draw "@pointsNum.txt" ^
-fill #00f ^
-draw "@edgeNum.txt" ^
-fill #080 ^
-draw "@triNum.txt" ^
%OUTLINES%
%IM%convert ^
-size %WW%x%HH% xc:None ^
-stroke #000 -fill None ^
-draw "@lines.txt" ^
-pointsize %PNTSIZE% -fill #a00 -stroke None ^
-undercolor rgba(100%%,100%%,100%%,0.5) ^
-fill #00f ^
-draw "@edgeNum.txt" ^
%OUTEDGES%
%IM%convert ^
-size %WW%x%HH% xc: ^
-fill rgba(75%%,75%%,100%%,0.5) ^
-draw "@tri.txt" ^
-stroke #000 -fill None ^
-draw "@lines.txt" ^
-pointsize %PNTSIZE% -stroke None ^
-fill #080 ^
-draw "@triNum.txt" ^
%OUTTRI%
%IM%convert ^
-size %WW%x%HH% xc:#000 ^
-fill #fff ^
-draw "@tri.txt" ^
-pointsize %PNTSIZE% -fill #f80 -stroke None ^
-draw "@pointsNum.txt" ^
%OUTCONV%
call echoRestore
@endlocal
This creates random points for tritst.exe.
It uses utility programs cSort.exe and cCount.exe. I don't provide the source or binaries of these.
rem Make Random Points, for exercising tritst.exe. rem rem %1 output filename rem %2 width rem %3 height rem %4 number of points rem %5 number of extra values per point (>= 0) set OUTFILE=%1 if "%OUTFILE%"=="" set OUTFILE=rand_pts.txt set TMPFILE=%TEMP%\mrp.lis set WW=%2 if "%WW%"=="" set WW=600 set HH=%3 if "%HH%"=="" set HH=400 set NumPts=%4 if "%NumPts%"=="" set NumPts=1000 set ValsPp=%5 if "%ValsPp%"=="" set ValsPp=3 set /A VPP2=%ValsPp%+2 (for /L %%i in (1,1,%NumPts%) do @( @%IM%identify -format "%%[fx:int(rand()*%WW%)] %%[fx:int(rand()*%HH%)]" xc: @for /L %%j in (1,1,%ValsPp%) do @%IM%identify -format " %%[fx:rand()]" xc: @%IM%identify -format "\n" xc: )) >%TMPFILE% rem Sort to remove duplicates, count them, ... cSort /i%TMPFILE% /o%TMPFILE% /f" " /k0-1 /u cCount /i%TMPFILE% /o%OUTFILE% echo %VPP2% >>%OUTFILE% rem ...then re-randomize the order. cSort /i%TMPFILE% /o- /f" " /k0-1 /Z >>%OUTFILE% type %OUTFILE%
All images on this page were created by the commands shown.
To improve internet download speeds, some images may have been automatically converted (by ImageMagick, of course) from PNG to JPG.
My usual version of IM is:
%IM%identify -version
Version: ImageMagick 6.9.1--6 Q16 x64 2015-06-20 http://www.imagemagick.org Copyright: Copyright (C) 1999-2015 ImageMagick Studio LLC License: http://www.imagemagick.org/script/license.php Features: Cipher DPC Modules OpenMP Delegates (built-in): bzlib cairo freetype jng jp2 jpeg lcms lqr openexr pangocairo png ps rsvg tiff webp xml zlib
This customised development version is:
%IMDEV%identify -version
Version: ImageMagick 6.9.0-0 Q32 x86_64 2015-10-10 http://www.imagemagick.org Copyright: Copyright (C) 1999-2014 ImageMagick Studio LLC Features: DPC HDRI Modules OpenMP Delegates (built-in): bzlib cairo fftw fontconfig freetype fpx jbig jng jpeg lcms ltdl lzma pangocairo png rsvg tiff webp x xml zlib
Source file for this web page is triangul.h1. To re-create this web page, execute "procH1 triangul".
This page, including the images, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.
Anyone is permitted to re-publish this page, but only for non-commercial use.
Anyone is permitted to link to this page, including for commercial use.
Page version v1.0 13-Feb-2015.
Page created 14-Oct-2015 04:02:02.
Copyright © 2015 Alan Gibson.