%IMG7%magick ^ -size 100x100 ^ xc:%col1% xc:%col2% xc:%col3% xc:%col4% ^ xc:%col5% xc:%col6% xc:%col7% xc:%col8% ^ +append +repage ^ pt_col_samp.png

Squares, triangles and hexagons.
ImageMagick can readily tile a rectangular raster image across a larger canvas. This page shows how other polygons can be tiled. In particular, tiling with squares, equilateral triangles and hexagons, either as solid colours or extracts from some image.
In the examples shown here:
The general technique is to build a prototype rectangle, and use that to tile a larger image.
We will use the following colours:
set col1=#b11 set col2=#118 set col3=#0a0 set col4=#818 set col5=#aa0 set col6=#0bb set col7=#f80 set col8=#80f
We make an image from those colours, just so we can see them:
%IMG7%magick ^ -size 100x100 ^ xc:%col1% xc:%col2% xc:%col3% xc:%col4% ^ xc:%col5% xc:%col6% xc:%col7% xc:%col8% ^ +append +repage ^ pt_col_samp.png |

|
set SqDim=100 %IMG7%magick ^ -size %SqDim%x%SqDim% ^ -stroke None ^ xc:%col1% xc:%col2% ^ +append ^ ( +clone -flop ) ^ -append ^ pt_sq1_proto.png %IMG7%magick ^ -size 1200x1200 ^ tile:pt_sq1_proto.png ^ -resize 50%% ^ pt_sq1_t.png
|
Prototype: pt_tri2.png |

|
|
tiled result: pt_tri2_t.png |

|
We set some environment variables for the triangles:
set IsoTriW=100 set IsoTriH=int(%IsoTriW%/2*sqrt(3)+0.5) rem Drawing starts at left-hand vertex, procedes clockwise. set IsoTriPoly=^ 0,0 ^ %%[fx:%IsoTriW%],0 ^ %%[fx:%IsoTriW%/2],%%[fx:%IsoTriH%] set IsoTriInvPoly=^ 0,%%[fx:%IsoTriH%] ^ %%[fx:%IsoTriW%/2],0 ^ %%[fx:%IsoTriW%],%%[fx:%IsoTriH%]
We make a prototype with the area of two triangles. Hence each of the two colours can occur exactly once.
%IMG7%magick ^ -size %%[fx:%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ +antialias ^ -fill %col1% -draw "polygon %IsoTriPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col2% -draw "polygon %IsoTriInvPoly%" ^ -fill %col1% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ pt_tri2.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri2.png ^ pt_tri2_t.png
|
Prototype: pt_tri2.png |

|
|
tiled result: pt_tri2_t.png |

|
As an alternative, we make a prototype with the area of four triangles. Hence each of the two colours can occur exactly twice.
%IMG7%magick ^ -size %%[fx:%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ +antialias ^ -fill %col1% -draw "polygon %IsoTriPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col2% -draw "polygon %IsoTriInvPoly%" ^ -fill %col1% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ pt_tri2_4.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri2.png ^ pt_tri2_4_t.png
|
Prototype: pt_tri2_4.png |

|
|
tiled result: pt_tri2_4_t.png |

|
We make a prototype with the area of four triangles. Hence each of the three colours can occur once or twice.
%IMG7%magick ^ -size %%[fx:%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ +antialias ^ -fill %col1% -draw "polygon %IsoTriPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col3% -draw "polygon %IsoTriInvPoly%" ^ -fill %col1% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ pt_tri3.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri3.png ^ pt_tri3_t.png
|
Prototype: pt_tri3.png |

|
|
tiled result: pt_tri3_t.png |

|
We make a prototype with the area of four triangles. Hence each of the four colours can occur exactly once.
%IMG7%magick ^ -size %%[fx:%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ +antialias ^ -fill %col1% -draw "polygon %IsoTriPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col3% -draw "polygon %IsoTriInvPoly%" ^ -fill %col4% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ pt_tri4.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri4.png ^ pt_tri4_t.png
|
Prototype: pt_tri4.png |

|
|
tiled result: pt_tri4_t.png |

|
We make a prototype with the area of eight triangles. Hence each of the six colours can occur exactly twice.
%IMG7%magick ^ -size %%[fx:2*%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ -fill %col1% -draw "polygon %IsoTriInvPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ -fill %col3% -draw "translate %%[fx:%IsoTriW%/2],0 polygon %IsoTriPoly%" ^ -fill %col4% -draw "translate %%[fx:%IsoTriW%],0 polygon %IsoTriInvPoly%" ^ -fill %col3% -draw "translate %%[fx:%IsoTriW%],%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ -fill %col4% -draw "translate %%[fx:%IsoTriW%/2],%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col1% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -fill %col2% -draw "polygon %IsoTriPoly%" ^ pt_tri4b.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri4b.png ^ pt_tri4b_t.png
|
Prototype: pt_tri4b.png |

|
|
tiled result: pt_tri4b_t.png |

|
We make a prototype with the area of eight triangles. Hence each of the six colours can occur either once or twice.
%IMG7%magick ^ -size %%[fx:2*%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ -fill %col1% -draw "polygon %IsoTriInvPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ -fill %col3% -draw "translate %%[fx:%IsoTriW%/2],0 polygon %IsoTriPoly%" ^ -fill %col4% -draw "translate %%[fx:%IsoTriW%],0 polygon %IsoTriInvPoly%" ^ -fill %col5% -draw "translate %%[fx:%IsoTriW%],%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ -fill %col6% -draw "translate %%[fx:%IsoTriW%/2],%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col1% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -fill %col2% -draw "polygon %IsoTriPoly%" ^ pt_tri6.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri6.png ^ pt_tri6_t.png
|
Prototype: pt_tri6.png |

|
|
tiled result: pt_tri6_t.png |

|
We make a prototype with the area of eight triangles. Hence each of the eight colours can occur exactly once.
%IMG7%magick ^ -size %%[fx:2*%IsoTriW%]x%%[fx:2*%IsoTriH%] ^ xc: ^ -fill %col1% -draw "polygon %IsoTriInvPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ -fill %col3% -draw "translate %%[fx:%IsoTriW%/2],0 polygon %IsoTriPoly%" ^ -fill %col4% -draw "translate %%[fx:%IsoTriW%],0 polygon %IsoTriInvPoly%" ^ -fill %col5% -draw "translate %%[fx:%IsoTriW%],%%[fx:%IsoTriH%] polygon %IsoTriPoly%" ^ -fill %col6% -draw "translate %%[fx:%IsoTriW%/2],%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -roll +%%[fx:%IsoTriW%/2]+0 ^ -fill %col7% -draw "translate 0,%%[fx:%IsoTriH%] polygon %IsoTriInvPoly%" ^ -fill %col8% -draw "polygon %IsoTriPoly%" ^ pt_tri8.png %IMG7%magick ^ -size %%[fx:6*%IsoTriW%]x%%[fx:6*%IsoTriH%] tile:pt_tri8.png ^ pt_tri8_t.png
|
Prototype: pt_tri8.png |

|
|
tiled result: pt_tri8_t.png |

|
We make a prototype with the area of six hexagons. Hence each of the three colours can occur exactly twice.
rem Half the hexagon width; length of each side. set HexRad=50 set HexH=(%HexRad%*sqrt(3)) rem Drawing starts at left-hand vertex, procedes clockwise. set HexPoly=^ 0,%%[fx:%HexH%/2] ^ %%[fx:%HexRad%/2],0 ^ %%[fx:%HexRad%*3/2],0 ^ %%[fx:%HexRad%*2],%%[fx:%HexH%/2] ^ %%[fx:%HexRad%*3/2],%%[fx:%HexH%] ^ %%[fx:%HexRad%/2],%%[fx:%HexH%] set HexPolyWd=^ 0,%%[fx:%HexH%/2] ^ %%[fx:%HexRad%/2-2],0 ^ %%[fx:%HexRad%*3/2+2],0 ^ %%[fx:%HexRad%*2+2],%%[fx:%HexH%/2] ^ %%[fx:%HexRad%*3/2+2],%%[fx:%HexH%] ^ %%[fx:%HexRad%/2-2],%%[fx:%HexH%] %IMG7%magick ^ -size %%[fx:3*%HexRad%]x%%[fx:%HexH%*3] ^ xc:%col2% ^ +antialias ^ -fill %col3% -draw "translate 0,%%[fx:%HexH%] polygon %HexPoly%" ^ -fill %col1% -draw "translate 0,%%[fx:%HexH%*2] polygon %HexPoly%" ^ -roll -%%[fx:%HexRad%*3/2]-%%[fx:%HexH%/2] ^ -fill %col1% -draw "polygon %HexPoly%" ^ -fill %col2% -draw "translate 0,%%[fx:%HexH%] polygon %HexPoly%" ^ -fill %col3% -draw "translate 0,%%[fx:%HexH%*2] polygon %HexPoly%" ^ pt_hex3.png %IMG7%magick ^ -size %%[fx:3*%HexRad%*3]x%%[fx:%HexRad%*sqrt(3)*4*1.5] ^ tile:pt_hex3.png ^ pt_hex3_t.png
|
Prototype: pt_hex3.png |

|
|
tiled result: pt_hex3_t.png |

|
In the above, we have drawn polygons filled with solid colours. Instead, we can fill with extracts from raster images.
In this section, we will translate portions of the source raster image. This means that in each polygon, the source raster image wil be painted "as it is", without rotating or reflecting the source.
The method is to make one raster image for each orientation of the polygon. That image is opaque at the polygon, and otherwise transparent. These raster images are used to build the prototypes, in a similar way to the solid-colour polygons above.
For squares, the prototype is the square, so the process is almost trivial.
|
Make the prototype: %IMG7%magick ^ toes.png ^ -gravity Center -crop 1:1+0+0 +repage ^ pt_sq.png |

|
|
Tile the prototype: %IMG7%magick ^ -size 1200x1200 ^ tile:pt_sq.png ^ -resize 50%% ^ pt_sq_t.png |

|
For triangles, we will build the raster images that correspond to the prototype pt_tri2.png:
|
Prototype: pt_tri2.png |

|
for /F "usebackq" %%L in (`%IMG7%magick ^ toes.png ^ -gravity center ^ -crop "%%[fx:%IsoTriW%]:%%[fx:%IsoTriH%]+0+0" +repage ^ -format "IsoTriRastW=%%w\nIsoTriRastH=%%h\n" ^ +write info: ^ pt_polyrect.png`) do set %%L echo IsoTriRastW=%IsoTriRastW% IsoTriRastH=%IsoTriRastH%
IsoTriRastW=267 IsoTriRastH=232
By coincidence, the aspect ratio of toes.png is almost exactly the same as the aspect ratio of an equilateral triangle.
set IsoTriRastPoly=^
0,0 ^
%%[fx:%IsoTriRastW%],0 ^
%%[fx:%IsoTriRastW%/2],%%[fx:%IsoTriRastH%]
set IsoTriInvRastPoly=^
0,%%[fx:%IsoTriRastH%] ^
%%[fx:%IsoTriRastW%/2],0 ^
%%[fx:%IsoTriRastW%],%%[fx:%IsoTriRastH%]
%IMG7%magick ^
pt_polyrect.png ^
+write mpr:PolyRect ^
+delete ^
( mpr:PolyRect ^
-fill Black -colorize 100 ^
+antialias -fill White -draw "polygon %IsoTriRastPoly%" ^
mpr:PolyRect ^
+swap ^
-alpha off -compose CopyOpacity -composite ^
-write pt_iso_tri_rast.png ^
+delete ^
) ^
( mpr:PolyRect ^
-fill Black -colorize 100 ^
+antialias -fill White -draw "polygon %IsoTriInvRastPoly%" ^
mpr:PolyRect ^
+swap ^
-alpha off -compose CopyOpacity -composite ^
-write pt_iso_tri_inv_rast.png ^
+delete ^
) ^
NULL:
|
pt_iso_tri_rast.png
|


|
Now we can build the prototype.
%IMG7%magick ^ -size %%[fx:%IsoTriRastW%]x%%[fx:2*%IsoTriRastH%] ^ xc: ^ +antialias ^ -fill %col1% -draw "image Over 0,0 0,0 pt_iso_tri_rast.png" ^ -fill %col1% -draw "image Over 0,%%[fx:%IsoTriRastH%] 0,0 pt_iso_tri_inv_rast.png" ^ -roll +%%[fx:%IsoTriRastW%/2]+0 ^ -fill %col1% -draw "image Over 0,0 0,0 pt_iso_tri_inv_rast.png" ^ -fill %col1% -draw "image Over 0,%%[fx:%IsoTriRastH%] 0,0 pt_iso_tri_rast.png" ^ pt_tri2_rast_tr.png %IMG7%magick ^ -size %%[fx:2*%IsoTriRastW%]x%%[fx:3*%IsoTriRastH%] tile:pt_tri2_rast_tr.png ^ pt_tri2_rast_tr_t.png
|
Prototype: pt_tri2_rast_tr.png |

|
|
tiled result: pt_tri2_rast_tr_t.png |

|
In the previous section, we built the prototype from polygons of a source raster image without rotation or reflection.
In this section, we will rotate and reflect the source raster, to obtain a mirroring effect at each edge.
For squares, we can automatically get the mirror effect from a -distort srt with a large viewport.
|
Tiled result: %IMG7%magick ^ pt_sq.png ^ -virtual-pixel Mirror -filter point ^ -set option:distort:viewport 1200x1200 ^ -distort srt 1,0 ^ -resize 50%% ^ pt_sq2_t2.png |

|
For triangles, we build the prototype from six polygons. Each polygon is a triangle, and they are the same triangle, rotated and reflected in six ways.
We build the prototype from six triangles, repeating each triangle, and we lay them out like this:
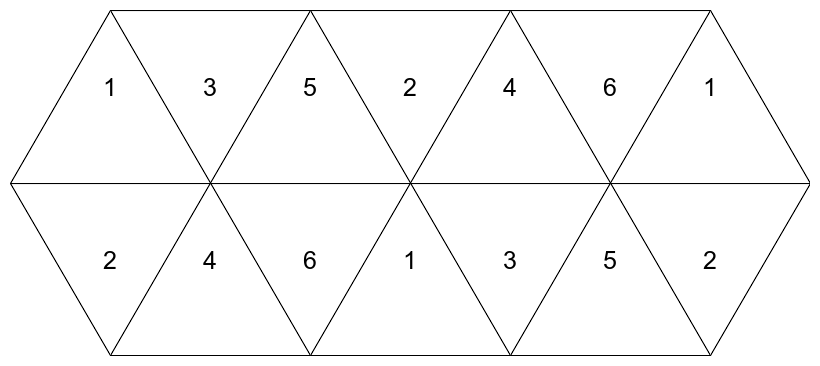
|
Here is the command that builds the prototype. It starts with a crop to the aspect ratio of an equilateral triangle. Triangles p1, p4 and p5 are made from this crop. p4 and p5 are rotations. Each of those three is given the opacity from a mask, to make the area to the left of the triangle transparent. The area to the right of the triangle will be overwritten by another triangle. This ensures we have no gaps between triangles. Those three triangles are flipped to make the other three triangles. The six triangles are appended in pairs. Each pair is composited in position with -layers mosaic. The left-most pair (p12) is repeated at the right side. Finally, a crop removes half of the left-most and right-most pairs.
%IMG7%magick ^
toes.png ^
-gravity Center ^
-crop 1:%%[fx:sqrt(3)/2]+0+0 +repage ^
-alpha off ^
-write mpr:CRP ^
-set option:WW %%w ^
-set option:HH %%h ^
-set option:Wm1 %%[fx:w-1] ^
( +clone ^
-fill Black -colorize 100 ^
+antialias -fill White -draw "polygon 0,%%[fx:h-1] %%[fx:(w-1)/2],0 %%[fx:w-1],0 %%[fx:w-1],%%[fx:h-1]" ^
-alpha off ^
-write pt_mask.png ^
-write mpr:MASK ^
+delete ^
) ^
( mpr:CRP ^
mpr:MASK ^
-compose CopyOpacity -composite ^
( +clone -flip ) ^
( -clone 0-1 ^
-append +repage ^
-write mpr:p12 +delete ^
) ^
+swap ^
-append +repage ^
-write mpr:p21 +delete ^
) ^
( mpr:CRP ^
-virtual-pixel Edge ^
+distort SRT 1,-120 +repage ^
-gravity NorthEast ^
-crop %%[WW]x%%[HH]+0+0 +repage ^
mpr:MASK ^
-compose CopyOpacity -composite ^
( +clone -flip ) ^
( -clone 0-1 ^
-append +repage ^
-write mpr:p43 +delete ^
) ^
+swap ^
-append +repage ^
-write mpr:p34 +delete ^
) ^
( mpr:CRP ^
-virtual-pixel Edge ^
+distort SRT 1,120 +repage ^
-gravity NorthWest ^
-crop %%[WW]x%%[HH]+0+0 +repage ^
mpr:MASK ^
-compose CopyOpacity -composite ^
( +clone -flip ) ^
( -clone 0-1 ^
-append +repage ^
-write mpr:p56 +delete ^
) ^
+swap ^
-append +repage ^
-write mpr:p65 +delete ^
) ^
-delete 0--1 ^
-compose Over ^
( -page +0+0 mpr:p12 ) ^
( -page +%%[fx:%%[WW]*0.5]+0 mpr:p34 ) ^
( -page +%%[fx:%%[WW]*1.0]+0 mpr:p56 ) ^
( -page +%%[fx:%%[WW]*1.5]+0 mpr:p21 ) ^
( -page +%%[fx:%%[WW]*2.0]+0 mpr:p43 ) ^
( -page +%%[fx:%%[WW]*2.5]+0 mpr:p65 ) ^
( -page +%%[fx:%%[WW]*3.0]+0 mpr:p12 ) ^
-layers mosaic ^
-crop %%[fx:%%[WW]*3.0]x+%%[fx:%%[WW]*0.5]+0 +repage ^
pt_toes_proto.png
Here is the prototype image, pt_toes_proto.png:

|
We can tile the prototype in the usual way:
%IMG7%magick ^ -size 1000x1000 ^ tile:pt_toes_proto.png ^ -resize 50%% ^ pt_toes_t.png |

|
Where the number of polygons that meet at each vertex is even, we can draw the same raster image in each polygon so that the polygons on each side of each edge are mirror-images.
This gives an algorithm for painting each pixel, taking the colour from a source location. For example, suppose the prototype is pt_tri2.png, and we want to paint pixels based on the blue triangle at top-middle.
|
Prototype: pt_tri2.png |

|
If the destination location is in the bottom half, then the first guess is by reflecting the location in the middle horizontal line. Assuming the orthogonal coordinates ii and jj are both in the range 0.0 to 1.0, with the origin at top-left, then:
if (jj > 0.5) {
jj = 1.0 - jj
}
If the destination location is in the small triangle top-left, then calculate ii and jj reflected in the nearest sloping boundary.
If the destination location is in the small triangle top-right, then calculate ii and jj reflected in that boundary.
The transformation from any area to the blue triangle can be represented by a 3x2 matrix. This can be composed from simpler transformations, eg rotate about the origin to make the mirror vertical, translate to put the mirror at jj=0, negate the jj-coordinate to reflect it, and finally reverse the translation and rotation. (Alternatively, use reflection as given in https://en.wikipedia.org/wiki/Rotations_and_reflections_in_two_dimensions .)
The condition for a location being within the top-left triangle is:
ii + jj < 0.5
To move the diagonal to pass through the origin, subtract 0.25 from ii and jj. Alternatively, subtract 0.5 from just ii or just jj.
Reflecting about the upper-left 45° line, the matrix is:
[ 0 -1 ]
M = [ ]
[ -1 0 ]
The general matrix for reflecting about a line at angle A is:
[ cos(2A) -sin(2A) ]
M = [ ]
[ +sin(2A) -cos(2A) ]
So:
if (ii + jj < 0.5) {
ii' = -(jj - 0.25) + 0.25 = -jj + 0.5
jj' = -(ii - 0.25) + 0.25 = -ii + 0.5
ii = ii'
jj = jj'
}
Alternatively, we initially subtract 0.5 from input x, and finally add 0.5 to output x:
if (ii + jj < 0.5) {
ii' = -jj + 0.5 = -jj + 0.5
jj' = -(ii - 0.5) = -ii + 0.5
ii = ii'
jj = jj'
}
... which is exactly the same.
For the upper-right triangle, the situation is symmetrical to the upper-right triangle. So we set iii=1.0-ii, and continue as above, remembering to reverse this transformation at the end.
The resulting values of ii and jj will be in the range 0.0 to 0.5, and within the upper triangle. Multiplying jj by 2.0 scales both coordinates to the range 0.0 to 1.0, so we can then multiply them by the dimensions of a source image (such as toes.png) to lookup source colours.
We put the above into an -fx operation like this. toes.png is 267 pixels wide.
set IsoTriW=267
set IsoTriH=int(%IsoTriW%/2*sqrt(3)+0.5)
set brW=%IsoTriW%
set brH=%IsoTriH%*2
set sFX=^
ii = i / (%brW%-1); ^
jj = j / (%brH%-1); ^
if (jj ^> 0.5, jj = 1-jj, ); ^
if (ii + jj ^< 0.5, ^
iip=0.5-jj; jj=0.5-ii; ii=iip, ^
); ^
iii = 1.0 - ii; ^
if (iii + jj ^< 0.5, ^
iip=0.5-jj; jj=0.5-iii; ii=1.0 - iip, ^
); ^
v.p{ii*v.w, 2*jj*v.h}
%IMG7%magick ^
-size %%[fx:%brW%]x%%[fx:%brH%] xc: ^
toes.png ^
-fx "%sFX%" ^
pt_tri2_rast.png
%IMG7%magick ^
-size %%[fx:%brW%*3]x%%[fx:%brH%*2] tile:pt_tri2_rast.png ^
pt_tri2_rast_t.png
|
Prototype: pt_tri2_rast.png |

|
|
tiled result: pt_tri2_rast_t.png |

|
All images on this page were created by the commands shown, using:
%IMG7%magick -version
Version: ImageMagick 7.1.1-20 Q16-HDRI x86 98bb1d4:20231008 https://imagemagick.org Copyright: (C) 1999 ImageMagick Studio LLC License: https://imagemagick.org/script/license.php Features: Cipher DPC HDRI OpenCL OpenMP(2.0) Delegates (built-in): bzlib cairo freetype gslib heic jng jp2 jpeg jxl lcms lqr lzma openexr pangocairo png ps raqm raw rsvg tiff webp xml zip zlib Compiler: Visual Studio 2022 (193532217)
To improve internet download speeds, some images may have been automatically converted (by ImageMagick, of course) from PNG or TIFF or MIFF to JPG.
Source file for this web page is polytile.h1. To re-create this web page, run "procH1 polytile".
This page, including the images, is my copyright. Anyone is permitted to use or adapt any of the code, scripts or images for any purpose, including commercial use.
Anyone is permitted to re-publish this page, but only for non-commercial use.
Anyone is permitted to link to this page, including for commercial use.
Page version v1.0 13-August-2024.
Page created 16-Aug-2024 15:37:38.
Copyright © 2024 Alan Gibson.